Conteggio

Il contare è un’attività che oggi appare del tutto istintiva, ma vi fu un tempo in cui l’essere umano non sapeva contare, almeno per il significato che oggi assume questa attività, né immaginava che si potesse fare o che avesse senso farlo. È stata una lenta conquista dell’essere umano acquisire il concetto di numero astratto, e in particolare di conteggio di una raccolta di elementi: la stessa conquista che vive un bambino che impara ad associare a una raccolta il numero dei suoi elementi, ossia la sua cardinalità.

Per riuscire a gestire un conteggio è necessario saper coordinare diverse componenti collegate a specifici contenuti matematici:

• la corrispondenza biunivoca, ossia il saper associare a ogni elemento di un insieme uno e un solo elemento di un altro insieme e viceversa. Nel contesto del conteggio, si tratta di saper collegare ogni parola-numero con ciascun oggetto da contare;
• la conta orale, ossia conoscere le parole-numero specifiche (i nomi dei numeri: uno, due, tre ecc.) della filastrocca o cantilena dei numeri. Competenza che si acquisisce in continuità tra scuola dell’infanzia e scuola elementare;
• l’enumerazione, l’azione di organizzazione spaziale di una collezione che permette di percorrerla in maniera controllata e ordinata, ossia di passare una e una sola volta da ogni elemento della collezione;
• la cardinalità dell’insieme, che consiste nel comprendere che l’ultima parola-numero pronunciata corrisponde alla numerosità dell’insieme contato.

In aggiunta a queste componenti, inoltre, è necessario anche saper coordinare tutte queste competenze con aspetti percettivo-motori.

L’attività di conteggio inizia fin da molto piccoli e rappresenta un argomento affrontato frequentemente durante gli anni di scuola dell’infanzia e in ambienti extrascolastici. Gli allievi all’ingresso della scuola elementare hanno così maturato diverse competenze, che variano da alunno ad alunno, e per le quali è necessaria una differenziazione delle proposte che tenga conto delle singole esigenze. Ci sono bambini capaci di gestire il conteggio di raccolte molto numerose, fino a 20 elementi o oltre, e altri che faticano anche con 3 o 4 elementi; non è quindi pensabile soprattutto per questo argomento fornire la stessa proposta a un’intera classe.

Sono tante le componenti del conteggio che devono essere acquisite e gestite dagli allievi. In particolare, il bambino dovrà essere in grado di coordinare contemporaneamente la parola, l’elemento della raccolta e il gesto (visivo o manuale). Tutti gli elementi dovranno essere considerati una e una sola volta secondo una strategia visuo-spaziale efficace, considerando le parole-numero corrette nel giusto ordine e, infine, sapendosi fermare quando si sono considerati tutti gli elementi.

Occorre tener conto che i bambini all’ingresso della scuola elementare contano con più precisione se usano il gesto, e se questo consente loro di toccare l’oggetto e, in caso di elementi mobili, di effettuare una partizione tra gli elementi già considerati e quelli ancora da considerare. Per alcuni allievi tali azioni non risultano però spontanee, in quanto entrano in gioco competenze visuo-spaziali, visuo-motorie, esecutive e di coordinazione difficili da essere gestite. Queste competenze vanno dunque considerate e favorite a livello didattico.

Se il bambino è in difficoltà con il conteggio, è importante che i docenti siano in grado di osservare questi diversi aspetti nel modo più preciso possibile, scomponendo le varie componenti richieste e considerando le diverse variabili (disposizione degli elementi, numero di elementi, natura degli elementi, distanza tra gli oggetti, dimensione dello spazio a disposizione ecc.) e modificando di conseguenza le situazioni proposte.

L’allievo potrebbe non essere capace di gestire la corrispondenza biunivoca perché associa ad alcuni elementi di un insieme un solo elemento di un altro insieme, o se ne dimentica altri. Questo avviene in particolare quando deve coordinare il ritmo della sequenza delle parole-numero con il gesto che indica un elemento da contare. Altri allievi potrebbero non conoscere la sequenza dei nomi dei numeri (la filastrocca dei numeri) per la raccolta considerata, quindi non essere in grado di associare il numero corrispondente agli elementi della raccolta. Altri allievi potrebbero non riuscire ad avere un piano di enumerazione efficace, con una strategia visuo-spaziale stabile e affidabile, che permetta loro di scegliere da dove partire, che strada seguire e dove fermarsi: passano più volte dagli stessi elementi, ne dimenticano alcuni o non riescono a gestire una partizione, ossia a separare gli elementi già contati da quelli ancora da considerare. Altri allievi potrebbero non sapersi fermare all’ultimo elemento dell’insieme, continuando a ricontare elementi già valutati. Altri ancora, pur riuscendo nelle singole componenti del conteggio, potrebbero non saperle coordinare in un tutto integrato, fallendo quindi quando si chiede di individuare il numero di elementi di una raccolta.

Avendo un’idea più precisa delle difficoltà degli allievi, sarà più facile attivare stimolazioni mirate o strategie compensatorie, creando percorsi personalizzati per sopperire alle diverse esigenze e per fornire proposte calibrate sulle reali competenze degli allievi. Tali considerazioni, oltre a riguardare il primo ciclo, sono trasferibili anche al secondo, modificando opportunamente le variabili in gioco di ogni componente del conteggio.

Tali oggetti sono gli stessi materiali che anche oggi si propongono in aula agli allievi per aiutarli a diventare abili nel conteggio. La pratica rudimentale di contare ricorrendo a sassolini presenti in natura si è poi raffinata soprattutto nei popoli del Medio Oriente (Sumeri, Assiri e Babilonesi) dove si iniziarono a creare piccoli oggetti in argilla detti calculi aventi forme prestabilite, da usare al posto dei sassolini. Calculi di diversa forma potevano così assumere valori diversi.

Dalla seconda metà del IV millennio a. C. alcuni di questi piccoli oggetti di forme e dimensioni differenziate venivano inseriti all’interno di contenitori ovoidali cavi in argilla, detti bolle; ciò allo scopo di quantificare ad esempio un debito, la registrazione di una proprietà, un pagamento effettuato. La chiusura della bolla e l’inserimento di un sigillo conferiva valore giuridico all’operazione. Per poter leggere il numero, occorreva quindi rompere la bolla. Per non dover ricreare ogni volta nuove bolle, a partire dal 3300 a. C. vennero rappresentati all’esterno i calculi racchiusi all’interno, ma così si perdette gradatamente la loro funzione iniziale; fu per questa ragione che le bolle furono in seguito sostituite dalle tavolette di argilla.

Va inoltre ricordato che le dieci dita della mano sono sempre servite all’essere umano per evocare i primi dieci numeri (da uno a dieci, escludendo lo zero, che può essere rappresentato con il pugno chiuso) e aiutare nelle tecniche di aritmetica elementare. Non è certo un caso che ancora oggi i bambini che iniziano a contare e a effettuare le prime operazioni sfruttino questo strumento o che gli adulti si aiutino con gesti che chiamano in causa le dita per accompagnare il loro pensiero, quando è enumerativo.

Contrariamente a quanto si può pensare istintivamente, le mani non sono servite per contare sempre solo fino a dieci. Una tecnica, diffusa in India, Indocina e nella Cina meridionale fino a pochi decenni fa, praticata su entrambe le mani con l’aiuto di un dito dell’altra, consisteva nel considerare ogni falange come unità. Si cominciava dalla falange inferiore del mignolo della mano destra per finire alla falange superiore del pollice di una stessa mano (è possibile anche cominciare dalla falange superiore del mignolo e terminare alla falangetta del pollice). Si poteva quindi andare da 1 a 14 su una sola mano e continuare il conto fino a 28 sull’altra.

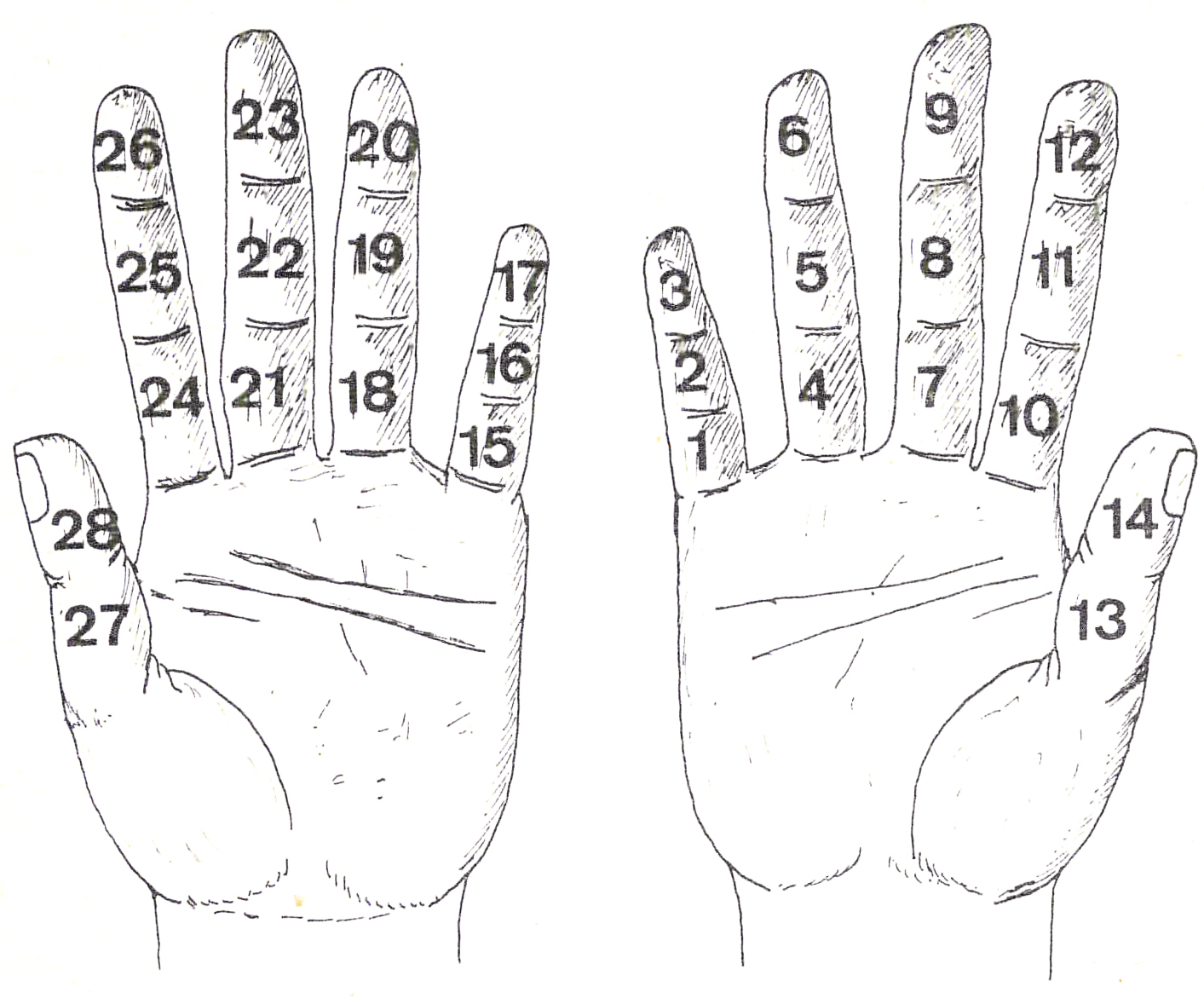
Un procedimento analogo, a lungo applicato nell’India nordorientale per pratiche religiose e tuttora in uso nelle provincie di Dacca (Bangladesh), di Calcutta (Bengala) e nei paesi islamici, dal Pakistan al Nord Africa, consiste nell’usare le giunture delle dita, cominciando dall’articolazione inferiore del mignolo e arretrando verso il pollice, il cui “grassello” vale come una giuntura. In questo modo, si può contare fino a 15 su una mano e fino a 30 su entrambe.

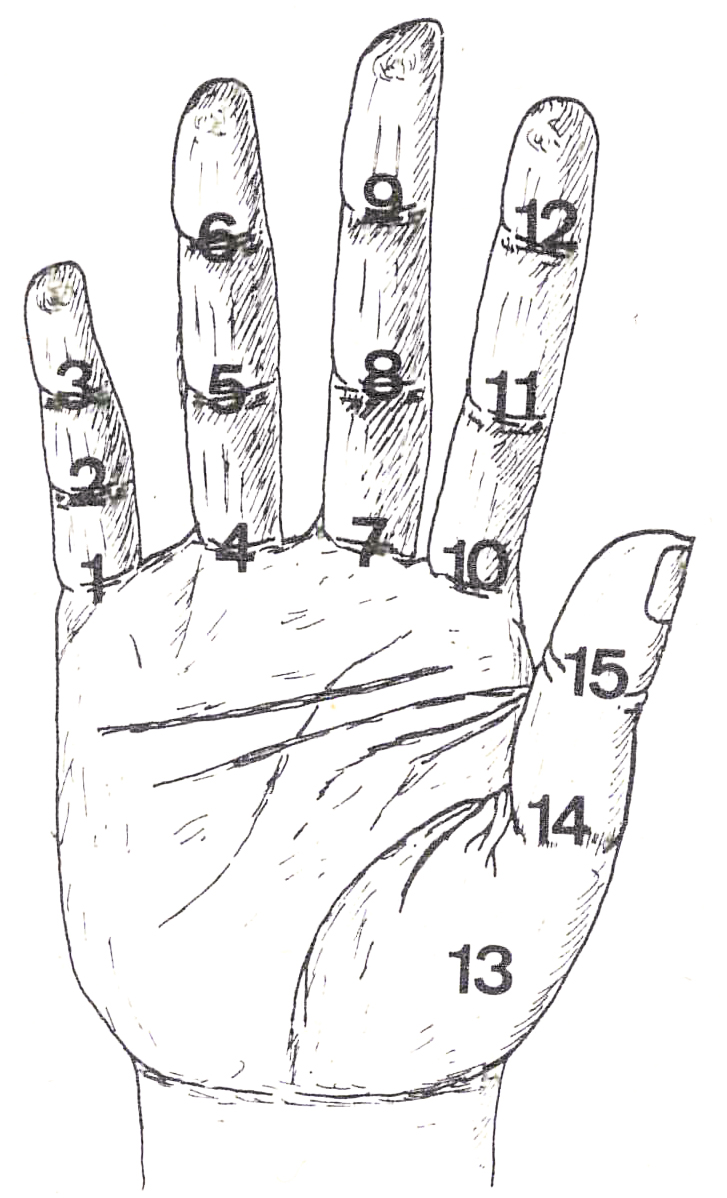
Tra le tecniche corporee connesse al numero, il ricorso alle dieci dita delle mani o alle diverse parti del corpo ha quindi svolto e svolge tuttora un ruolo determinante e la mano può essere considerata come la più semplice e disponibile macchina calcolatrice impiegata da tutte le popolazioni nel corso delle ere.