Corrispondenza biunivoca

La corrispondenza uno a uno, detta corrispondenza biunivoca, è un’abilità che permette di confrontare la numerosità di due raccolte di oggetti, senza far ricorso a un procedimento astratto quale il conteggio, la nominalizzazione delle quantità o la conoscenza delle quantità implicate.

Si tratta di associare ad ogni elemento di un insieme uno e un solo elemento di un altro insieme e viceversa. Rappresenta un’operazione di pre-calcolo con la quale il bambino si trova confrontato quotidianamente. Ad esempio, nel ballo tradizionale c’è un maschio per ogni femmina; quando deve apparecchiare la tavola c’è un piatto per ogni tovagliolo; per ogni allievo c’è un banco in aula ecc.

Il bambino all’età di 2 anni inizia già spontaneamente ad applicare la corrispondenza biunivoca di fronte a collezioni di oggetti tridimensionali complementari, come ad esempio abbinare l’animale alla sua casa, distribuire un giocattolo ad ogni persona ecc.

Il gesto aiuta i bambini a realizzare la corrispondenza biunivoca, consentendo di tener traccia degli elementi considerati; è possibile lasciare anche dei supporti come pennarelli, corde o altro materiale per consentire di realizzarla con più facilità.

La corrispondenza biunivoca diventa più complessa a seconda della tipologia di oggetti considerati (ad esempio si complica passando da oggetti complementari come: uovo-portauovo; pennarelli e tappi ecc. a non complementari), delle loro dimensioni, da come sono disposti (oggetti in fila o non in fila, essendo in quest’ultimo caso confrontati con il concetto della conservazione della quantità) ecc. Se si considerano ad esempio oggetti eterogenei ma complementari, come uovo-portauovo, posti uno di fronte all’altro come nella figura seguente, i bambini di solito non riscontrano particolari difficoltà nell’abbinare gli elementi uno a uno e nel sostenere quindi che i due insiemi hanno la stessa quantità di elementi.

Se invece vengono distanziati gli oggetti di una delle due collezioni, i bambini possono avere difficoltà nell’abbinarli percettivamente, non rendendosi conto che la quantità degli elementi non cambia al variare della loro disposizione spaziale.

Di fronte a due insiemi disposti in modo non allineato subentra infatti la difficoltà di effettuare un’esplorazione completa e senza ripetizione degli elementi di ciascun insieme, che presuppone una competenza che i bambini potrebbero avere difficoltà a gestire.

L’equivalenza quantitativa di due insiemi costituiti dallo stesso numero di elementi è un concetto che il bambino costruisce progressivamente, grazie alle proposte didattiche e al suo sviluppo intellettuale.

Va tenuto conto che la corrispondenza biunivoca rappresenta una strategia utile per confrontare la numerosità di due insiemi a qualsiasi livello scolastico. Per convincersene è sufficiente ricordare che la corrispondenza biunivoca è proprio la strategia che consente di confrontare due insieme infiniti, come l’insieme dei numeri naturali  e l’insieme dei numeri pari P, permettendo di scoprire che hanno la stessa quantità di elementi, ossia la stessa cardinalità. Corrispondenza biunivoca che è bene presentare agli allievi fin dal secondo ciclo.

Fu proprio grazie alla corrispondenza biunivoca che l’uomo preistorico, nel corso di millenni, riuscì a costruire e poi utilizzare l’aritmetica per sopperire ad esigenze pratiche di contabilità, classificazione e distribuzione, ben prima di giungere all’idea di numero astratto.

Basta immaginare un pastore che sorveglia un gregge di pecore e che, per controllarle al rientro nella caverna, le fa entrare una alla volta; per ciascuna che gli passa davanti, intaglia una tacca su un bastone, oppure tiene il bastone saldamente in mano e fa scorrere l’unghia del pollice sulle tacche già incise, una per ogni pecora rientrata. In questo modo, potrà controllare ogni giorno, enumerando a una a una ciascuna pecora, se il suo gregge è al completo.

Questo metodo di conteggio basato sugli intagli è sicuramente uno dei più antichi; le prime testimonianze archeologiche note di tale pratica risalgono al 35'000 a. C. Si tratta del ritrovamento di diverse ossa e pietre oblunghe, recanti una o più successioni di incisioni regolarmente separate, rintracciate prevalentemente nell’Europa occidentale.

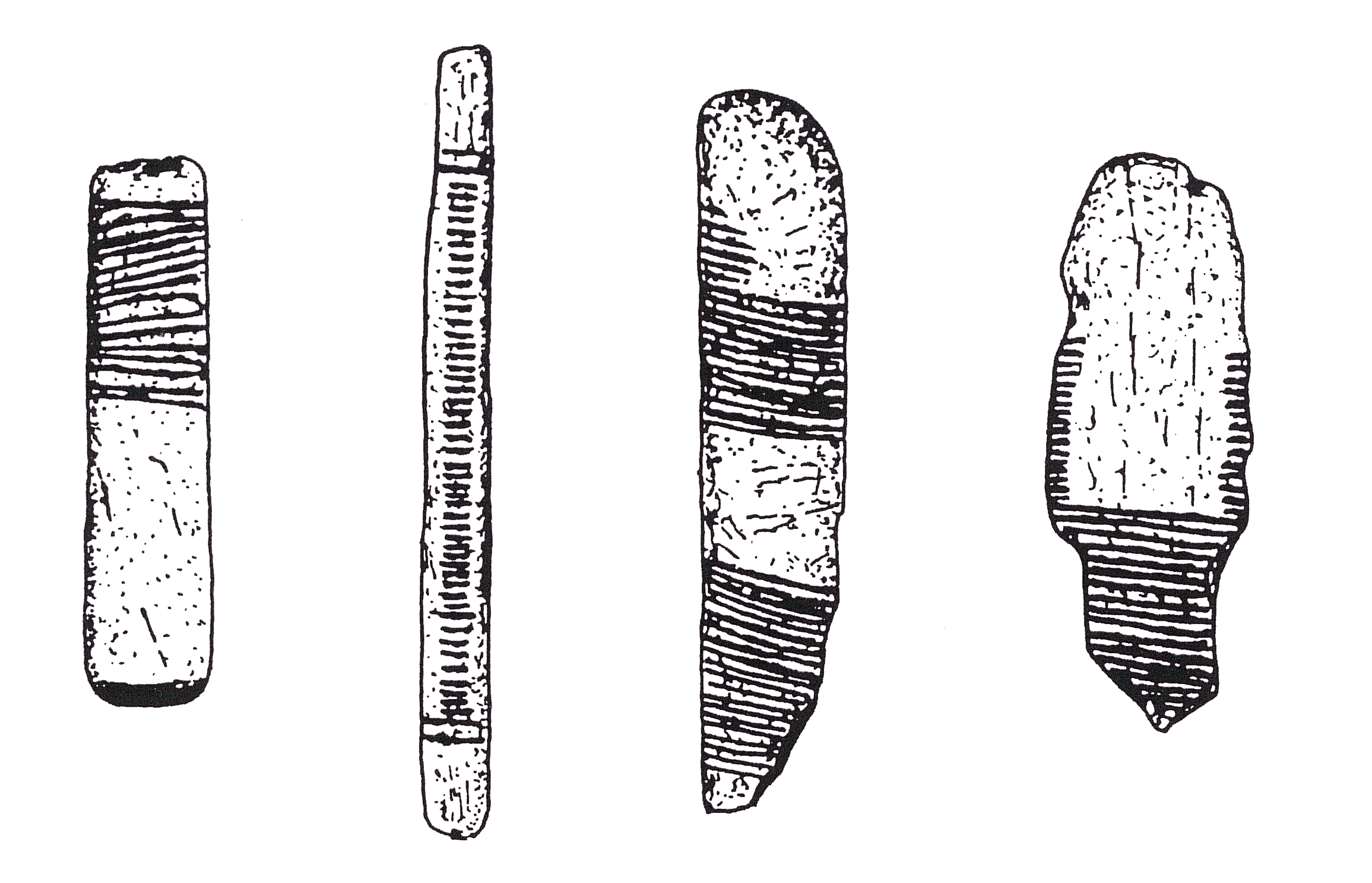
La corrispondenza biunivoca ha la proprietà di non tener conto della natura degli oggetti dei due insiemi considerati, valendosi così di un’azione astratta che esprime una caratteristica comune alle due raccolte in questione. Così facendo, con 15 tacche su un bastone è possibile considerare raccolte di 15 pecore, 15 vasi, 15 frecce, 15 nemici, 15 frutti, 15 pesci, 15 guerrieri ecc. indipendentemente dunque dal tipo di oggetti specifici che costituiscono la raccolta.

Nella storia della matematica la corrispondenza biunivoca è sempre servita per confrontare numerosità e ha avuto un ruolo determinante per confrontare insiemi infiniti. Ricordiamo ad esempio il matematico Ruggero Bacone, che nella sua opera Opus Maius del 1233 scrisse che si può stabilire una corrispondenza (biunivoca, diremmo noi oggi) tra i punti di un lato di un quadrato e i punti di una diagonale dello stesso, nonostante abbiano diversa lunghezza. Basta osservare la seguente figura nella quale, immaginando di muovere la freccia OP', a ogni punto P del lato viene fatto corrispondere uno e un solo punto P' della diagonale, analogamente, ad ogni punto Q della diagonale viene fatto corrispondere un solo punto Q' del lato.

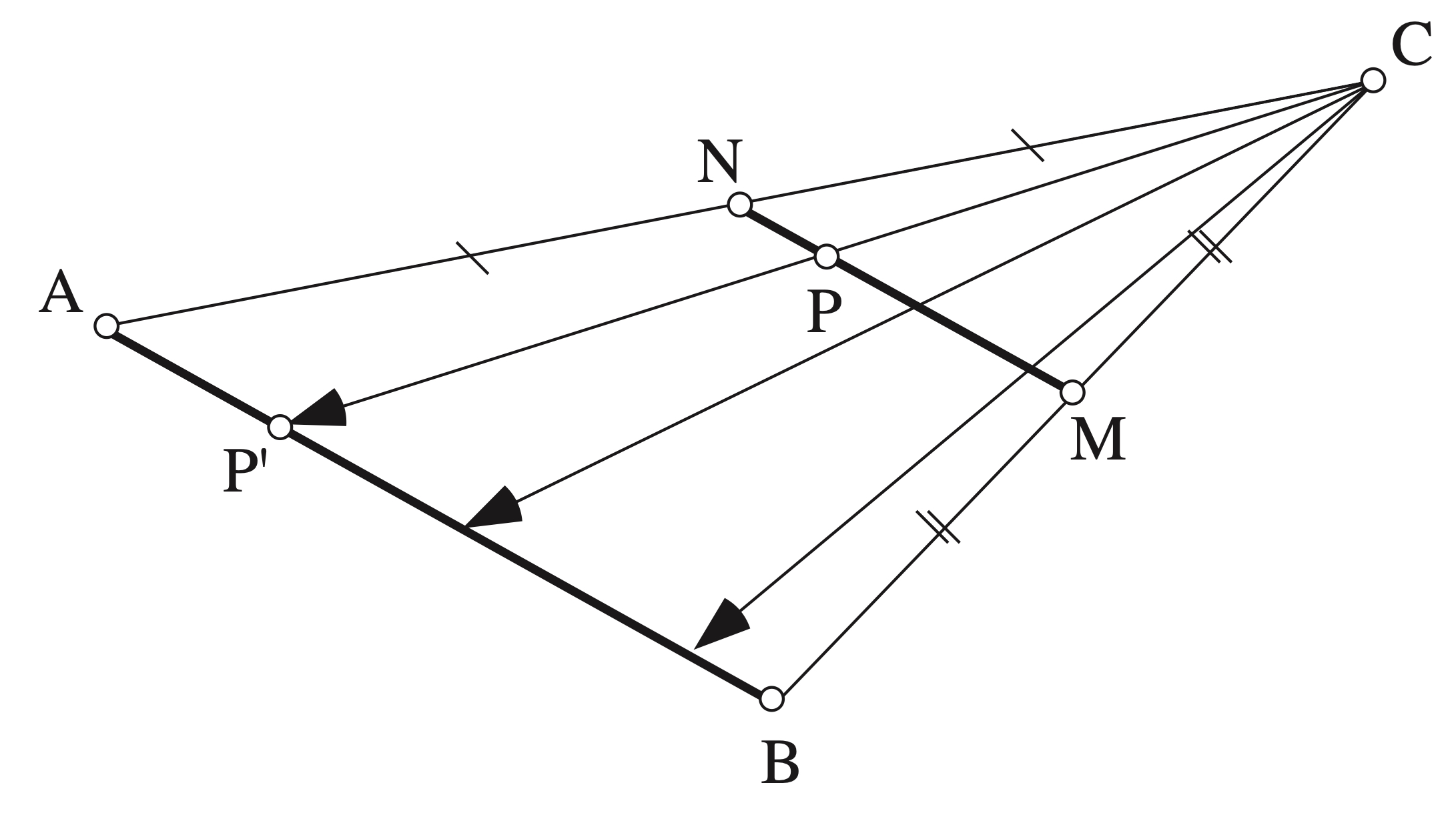
Bacone non è il solo ad essersi occupato di infinito e corrispondenze biunivoche. Il grande Galileo Galilei, ad esempio, osservò che basta disegnare un triangolo ABC e vedere che tra il lato AB e il segmento NM, che congiunge i punti medi degli altri due lati, deve esistere una corrispondenza biunivoca ottenuta congiungendo i punti di AB con C e considerando il punto P' di AB, corrispondente di P di MN, ottenuti come intersezione di MN con CP'. Tutto ciò contro l’intuizione che sembra portare a far credere che AB, dato che ha lunghezza doppia rispetto a MN, sia formato da un numero maggiore di punti (si veda la figura).

Anche in questo caso, osserviamo che vale anche il viceversa, ossia preso un qualsiasi punto Q appartenente al segmento più corto MN, lo si potrebbe collegare a C; prolungando CQ fino ad intersecare il segmento più lungo AB si troverebbe uno e un solo punto Q', corrispondente di Q.

Grazie a considerazioni di questo tipo si arriva dunque a scoprire che l’infinito può entrare in collisione con la famosa “nozione comune” di Euclide: «Il tutto è maggiore della parte».

Galilei propose analoghe considerazioni anche in ambito numerico. Famosa è la costatazione detta paradosso di Galilei, nel quale si afferma che, da una parte, l’insieme ℕ_Q dei numeri naturali quadrati è un sottoinsieme dell’insieme ℕ dei numeri naturali, ma che, d’altra parte, è facile stabilire una corrispondenza biunivoca fra ℕ e ℕ_Q facendo, per esempio, corrispondere a ogni numero n il suo quadrato n²:

Nella seconda metà del 1800 Georg Cantor, la figura di maggior spicco nel campo degli insiemi infiniti, mostrò tramite corrispondenze biunivoche che ci sono tanti numeri naturali ℕ, quanti razionali ℚ, quanti interi ℤ: la cardinalità di questi insiemi è l’infinito numerabile. È solo nell’insieme dei numeri reali ℝ che si ha a che fare con un altro tipo di infinito, l’infinito del continuo.