Frazioni
Il tema delle frazioni è uno degli argomenti numerici più ampi e complessi della scuola elementare, in continuità con la scuola media.
Consideriamo tutti i numeri naturali ℕ e poi tutte le scritture del tipo a/b, dove sia a sia b sono numeri naturali, per esempio: 1/2, 3/5, 7/7, 9/3, 0/5, 4/12, …
Tutte queste scritture aritmetiche sono frazioni, che non sono altro che un modo di rappresentare i numeri razionali. Abbiamo infiniti modi di rappresentare un numero razionale tramite le frazioni, grazie alle frazioni equivalenti. Inoltre, la frazione a/b rappresenta la divisione a : b, quindi b non può essere 0, dato che lo 0 non può mai essere un divisore. Infatti, consideriamo un qualsiasi numero naturale a non nullo; se si potesse dividere a per 0, allora esisterebbe un numero razionale c, tale che c × 0 = a. Ma questo sarebbe possibile solo se a fosse 0, e questo genera una contraddizione (si veda il contenuto Divisione). La sesta frazione (4/12) ridotta ai minimi termini è 1/3. Facciamo inoltre notare che la terza frazione nell’elenco precedente (7/7) può essere pensata come una rappresentazione del numero 1, la quarta frazione (9/3) del 3, la quinta frazione (0/5) dello 0, tornando così ai numeri naturali. È allora ovvio che tutti i numeri naturali si possono pensare come frazioni un po’ speciali.
Consideriamo la frazione a/b: il numero a è detto numeratore, mentre b è detto denominatore.
Si noti che se abbiamo due frazioni equivalenti, come 3/4 e 9/12, allora 3 × 12 = 9 × 4. Questo perché due frazioni equivalenti individuano un’uguaglianza di rapporti: 3/4 = 9/12 che non è altro che una proporzione (argomento che gli allievi approfondiranno in seguito alla scuola media).
Per valutare se è più grande una frazione o un’altra, basta trovare due frazioni con lo stesso denominatore equivalenti alle due frazioni date e poi confrontare i numeratori. Per confrontare ad esempio 2/3 e 3/4 si può trovare il minimo comune multiplo dei due denominatori (12); oppure si può banalmente moltiplicare per 4 sia il numeratore sia il denominatore della prima frazione; e poi moltiplicare per 3 sia il numeratore sia il denominatore della seconda frazione; si otterranno così le due frazioni: 8/12 e 9/12 che sono equivalenti a quelle precedenti. Si vede subito allora che la seconda frazione è più grande della prima, perché 9 è maggiore di 8. Nel proporre questo argomento occorre essere consapevoli che vi sono diverse interpretazioni di tale concetto, legate ai diversi contesti d’uso di tali numeri. Alcune interpretazioni sono più specifiche per la scuola elementare, altre vengono affrontate formalmente nei livelli scolastici successivi, anche se possono essere intuite anche alle elementari, soprattutto se legate al vissuto che circonda gli allievi.
Aspetti didattici
Quando si parla di frazioni nella scuola elementare è importante partire dalle convinzioni che hanno gli allievi su questo argomento, valorizzando l’uso di tale tema nel contesto reale. L’interpretazione che emerge inizialmente è quasi esclusivamente basata sulla relazione parte-tutto, inerente oggetti principalmente continui (una torta, una pizza, una mela ecc.), ma anche discreti (un insieme di palline, bambini, figurine ecc.), con tante e imprevedibili interpretazioni diverse: tanti pezzi che si ottengono dalla divisione di un oggetto; ciascuna delle due parti non per forza congruenti che si ottengono tagliando; la linea che separa due parti; l’azione di suddividere ecc. Per molti bambini l’aspetto rilevante del significato di metà è che “le parti” siano due, puntando così l’attenzione sull’aspetto numerico, senza considerare la congruenza delle parti: «È la parte della terra dove è giorno o quella dove è notte» (5 anni).

I bambini dei primi anni di scuola elementare, dovendo colorare metà della superficie di un quadrato rappresentato su un foglio a quadretti, scelgono spesso di farlo in base al numero di quadretti, piuttosto che alla congruenza delle parti, se questa non è già stata imposta da una definizione vincolante.
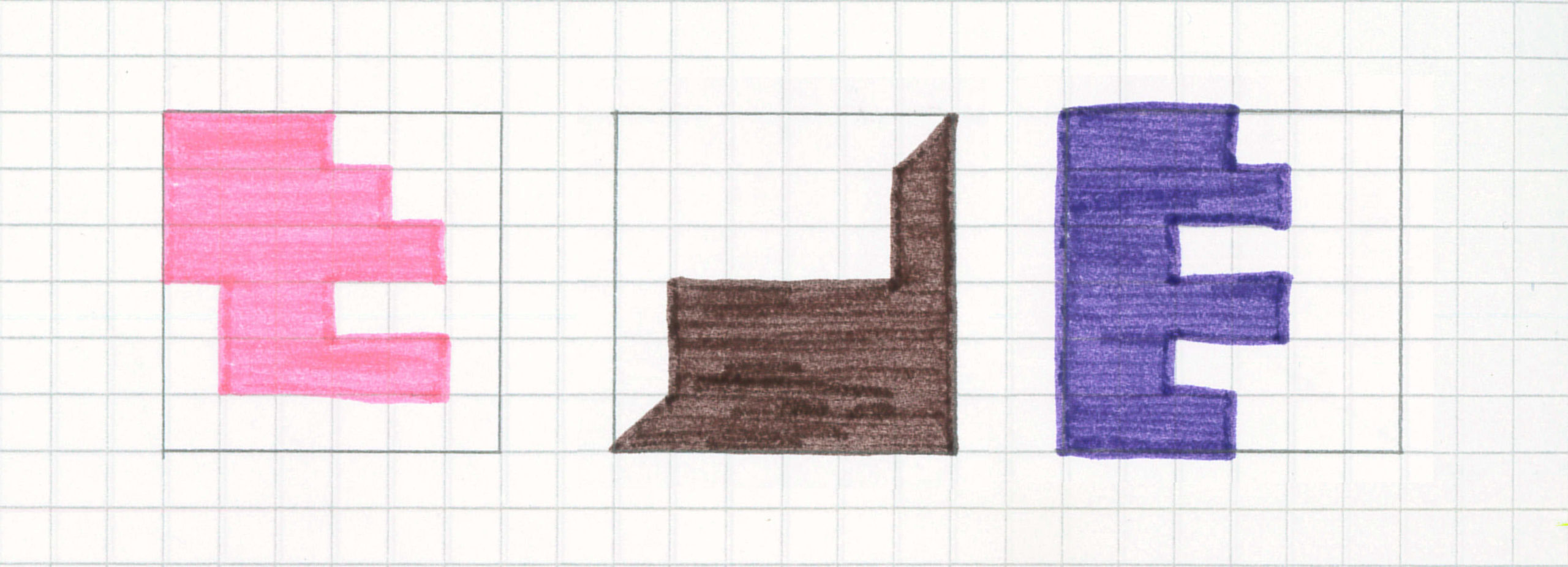
Spesso infatti, si sceglie di introdurre questo argomento partendo dalla seguente definizione: “frazionare vuol dire dividere in parti uguali”, che risulta però essere vincolante rispetto ai molteplici significati del concetto e addirittura erronea, dato che la parola “uguale” (intesa come congruente) non consente di accettare che gli oggetti o figure siano divisi in parti di forma diversa, pur rispettando proprietà (come ad esempio l’equinumerosità, l’isoperimetria, l’equiestensione, l’equivolumetria ecc.). Ad esempio, nella figura seguente, la parte colorata rappresenta 1/4 dell’area dell’intero rettangolo, anche se la figura non è stata divisa in parti “uguali”.
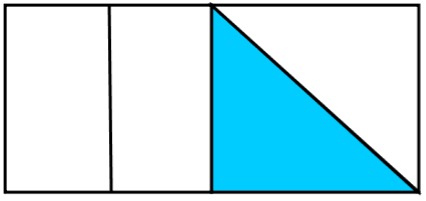
D’altronde ciò avviene anche nella vita reale: un qualsiasi pezzo di torta che decidiamo di mangiare rappresenta una frazione dell’intero, anche se in precedenza la torta non è stata tagliata in parti uguali! Nella scuola elementare risulta quindi molto importante proporre agli allievi ricche e significative situazioni, in vari contesti discreti e continui, che contemplano la frazione parte-tutto applicata a diverse proprietà, e non esclusivamente alla congruenza delle parti.
Nel continuo, quando si passa dal reale a considerare frazioni di figure astratte, non vanno proposte solamente forme facili da frazionare, ma anche “stravaganti”, per non generare la misconcezione che solo nelle figure standard si possono trovare frazioni. La “stravaganza” può essere ricercata anche nelle forme delle parti che si individuano. Per motivare i bambini nella ricerca di partizioni, è possibile creare un concorso di classe per premiare la più originale suddivisione di un intero in parti che rispettano una certa proprietà.
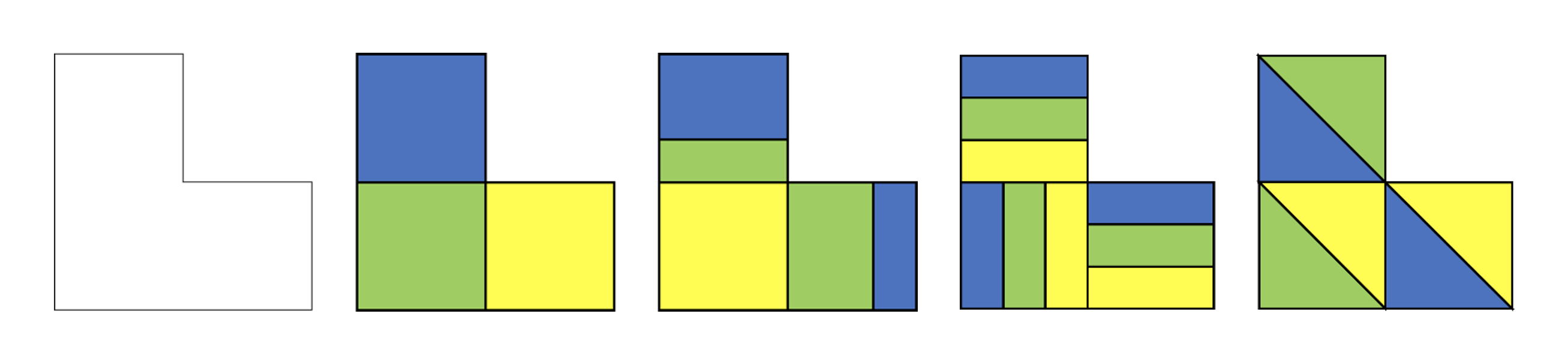

Può essere anche interessante far notare che l’unità continua si può sempre frazionare solo in teoria, perché dividere concretamente un foglio in 120/379, non è una cosa semplice da ottenere nella pratica. Inoltre, quando si parla di frazioni nel discreto, vale la pena non limitarsi a chiedere di trovare suddivisioni possibili, ma può essere anche interessante ragionare su quelle impossibili. Per esempio, se si considera un insieme di 12 persone, si possono trattare non solo 1/2 o i 2/3 (la totalità delle persone è multiplo di 2 e di 3), ma si può considerare anche 1/5 di tale insieme per scoprire che è impossibile da trovare in concreto, essendo una situazione che dal punto di vista semantico non è attuabile.
Inoltre, quando si propone tale interpretazione della frazione (parte-tutto) è importante considerare non soltanto situazioni didattiche che prevedono attività dal tutto alla parte, ma anche dalla parte al tutto. Sarebbe inoltre didatticamente importante far vivere agli allievi un’ampia gamma di esperienze legate ai diversi aspetti di questo ricco oggetto matematico, ma va considerato che le frazioni possono rappresentare un argomento molto ostico se affrontato con un approccio troppo formale e lontano dal vissuto degli allievi.
A volte la frazione a/b rappresenta un quoziente, una divisione non necessariamente effettuata, ma solo indicata a : b; in questo caso l’interpretazione più intuitiva è la seguente: abbiamo a oggetti e dividiamo ciascuno in b parti. Ad esempio, se abbiamo un insieme discreto di 6 oggetti e ne dobbiamo prendere i 3/5, una tecnica può essere quella di dividere ogni elemento in 5 parti e poi prenderne 3 di tali quinti da ciascun oggetto, sempre che questi oggetti si passano dividere!
A volte la frazione è considerata come un operatore moltiplicativo, per esempio “Trovare i 4/5 dell’insieme di 20 persone”, in questo caso si opera nel seguente modo: (20 : 5) × 4 persone. Si agisce combinando la divisione e la moltiplicazione, dunque operando sui numeri puri invece che sulle raccolte e sugli oggetti.
Nelle ricette culinarie è possibile sperimentare praticamente la frazione come rapporto, mostrando così un legame tra grandezze, trovandosi a dover calcolare e preparare le quantità di ingredienti in relazione al numero delle persone da considerare.
Nella probabilità si tratta di esprimere, attraverso una frazione, il numero di casi favorevoli all’evento rispetto al numero dei casi possibili, ed è possibile creare situazioni di questo tipo sfruttando monete, dadi, biglie.
Un altro aspetto da contemplare è la frazione come misura: “3/4 di un litro, 1/4 di litro, 1/2 litro”; “La misura delle mie scarpe è 35 e 1/2”; “Ieri avevo 37 e 1/2 di febbre”. Queste affermazioni mettono in evidenza delle vere e proprie misure. Un ulteriore esempio in questo senso legato al lessico comune è l’affermazione: “Sono le quattro e un quarto”, dove un quarto, rappresenta una frazione di un’ora, ma nell’uso comune vuol dire 15 minuti, ossia rappresenta un riferimento specifico: “La lancetta lunga sta sul 3 del nostro orologio, si trova in quella posizione”.
Anche la percentuale non è altro che una frazione, con peculiarità specifiche (“sconto del 50%”, “una pendenza del 10%”).
C’è un momento in cui la frazione viene posizionata su una retta orientata e acquista un nuovo significato, ma ciò viene trattato nella scuola media. Nella scuola elementare si può valutare se una frazione è minore di un’altra, cercando di lavorare didatticamente sulle possibili misconcezioni che si possono generare e aiutandosi eventualmente con diverse rappresentazioni. Per esempio, 2/3 può essere ritenuta inizialmente minore di 4/9, perché i bambini, confrontando inizialmente solo i numeratori, desumono che 2 è minore di 4 (e anche che 3 è minore di 9), così come avviene nei numeri naturali. Altri credono che ciò avvenga per l’analogia con i numeri decimali: 2,3 è minore di 4,9 perché 2 è minore di 4, allora sarà così anche tra 2/3 e 4/9. Su tali misconcezioni si può intervenire facendo vivere situazioni concrete dove vengono visualizzate le frazioni o dove è importante ricorrere a frazioni equivalenti; in questo caso, portando le frazioni ad avere lo stesso denominatore, si ottengono le frazioni 6/9 e 4/9 a confronto.
Gradualmente, grazie a tutte queste esperienze che si susseguono nei vari livelli scolastici, la frazione dovrà trasformarsi in numero razionale, assumendo un nuovo complesso significato.
Cenni storici
La storia dei numeri razionali è molto antica, soprattutto la rappresentazione in forma frazionaria di tali numeri. Le frazioni sono state infatti concepite nelle diverse epoche e nelle varie culture. L’idea di frazione appare esplicitamente su tavolette sumere del 4000 a. C., mentre una vera e propria teoria delle frazioni è presente nei papiri egizi.
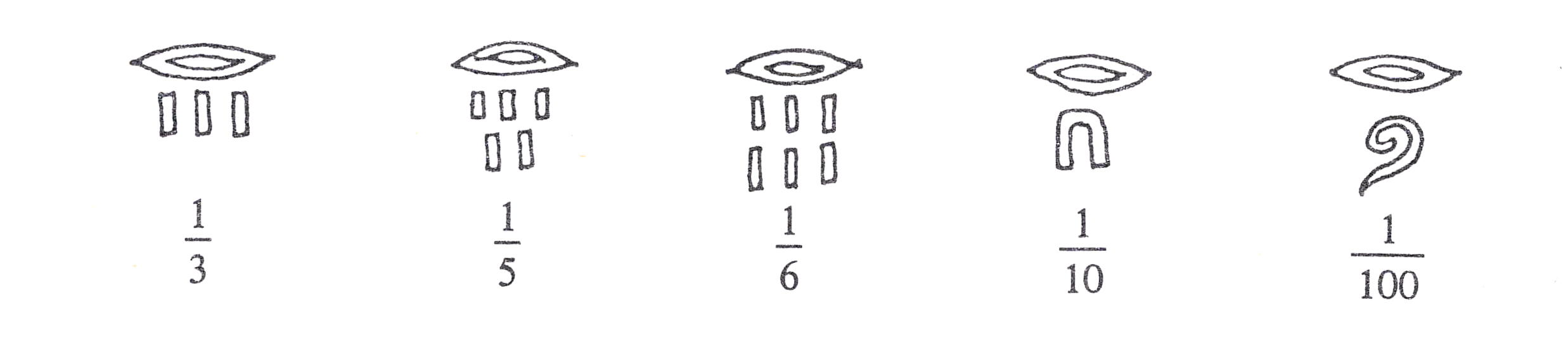
Questi ultimi dedicarono molta passione allo studio delle frazioni dove furono maestri insuperati fino al Medioevo. Ad esempio, nel famoso documento matematico dell’antico Egitto: il cosiddetto “papiro di Ahmes” o “di Rhind” del 1650 a. C., vi erano 84 problemi di matematica risolti e varie questioni aventi a che fare con le frazioni. Le scritture geroglifiche delle frazioni sono molteplici, proponiamo di seguito la più nota.
Il segno superiore che appare in tutti è il segno geroglifico “bocca” che si legge èr e che significa “parte”; esso funge dunque da numeratore unitario del tipo 1/ . Il numerale che appare sotto la bocca è il denominatore. In passato si pensava che gli Egizi usassero solo frazioni “unitarie” (che, infatti, spesso sono dette “frazioni egizie”), ma in realtà utilizzavano anche altre due frazioni, 2/3 e 3/4, alle quali riservavano simboli particolari:
per 2/3:
per 3/4:
È vero, però, che gli Egizi non considerarono mai 2/3 e 3/4 come vere e proprie frazioni, ma piuttosto come simboli divini.
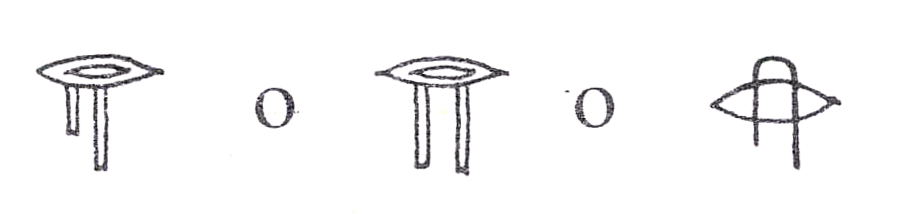
Anche la frazione 1/2, per la sua peculiarità indiscutibile, aveva un segno geroglifico a parte:

oppure il seguente:

che si chiamava ghes cioè “metà”.
I papiri rivelano che gli Egizi furono veri e propri maestri a ridurre frazioni complesse in frazioni unitarie. Per esempio, si trovano, tra mille altri esempi, le seguenti uguaglianze:
3/5=1/2+1/10,
47/60=1/3+1/4+1/5,
naturalmente i primi membri delle uguaglianze erano espressi o dal contesto o a parole.
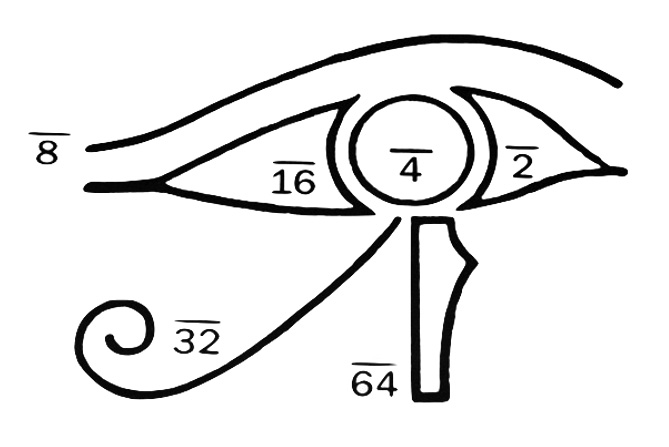
Le frazioni egizie hanno anche un ruolo particolare nel mito e nelle leggende, come il famoso mito di Horus del 2000 a. C. circa. Tale mito ha moltissime varianti, una delle quali parla della dispersione per vendetta dei frammenti dell’occhio del Dio nel deserto. L’occhio venne diviso una prima volta a metà, poi ancora a metà e così di seguito per sei volte, fino ad avere un pezzetto che rappresenta 1/64 di tale organo. La figura stilizzata di tale occhio, null’altro è se non una scrittura ieratica delle frazioni.
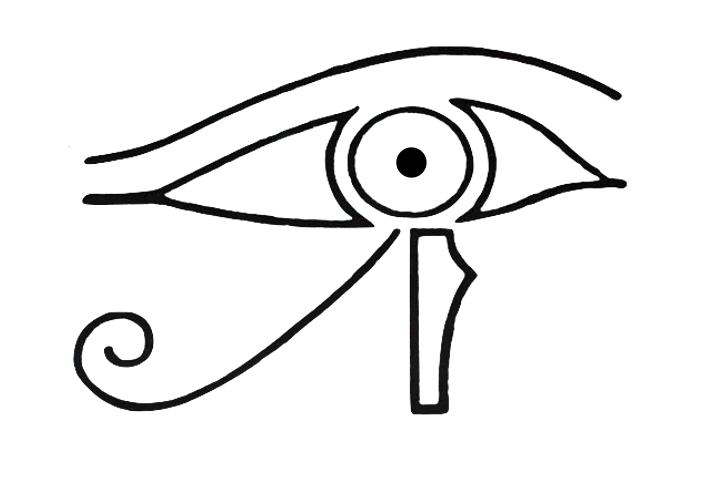
In effetti, gli Egizi del 2000 a. C. scrivevano le frazioni nel seguente modo:
A questo punto, la leggenda afferma che una splendida fanciulla, impietosita, e con grande atto d’amore, raccolse i vari pezzetti dell’occhio, da 1/2 fino ad 1/64, e li reinserì con cura e con affetto nella cavità oculare rimasta vuota di Horus; fatto ciò, Horus riprese la vista ed amò per sempre la fanciulla.
Ma la somma proposta dalla leggenda, 1/2+1/4+1/8+1/16+1/32+1/64, non ridà l’occhio per intero, cioè non ha come somma 1, dato che, comunque, manca 1/64. Si ipotizza dunque che la storia, al di là del mito dell’amore compassionevole, volesse richiamare l’attenzione sul calcolo frazionario che gli Egizi consideravano sacro.
Anche nella faticosa aritmetica greca si concepirono le frazioni. Per rappresentarle si faceva ricorso all’apostrofo; per esempio, tenendo presente che β rappresentava il 2 e che γ rappresentava il 3, β’ significa 1/2 mentre γ’ significa 1/3. Questo fatto creava però ambiguità. Per esempio, la scrittura πε’ poteva voler dire tanto 80/5 quanto 1/85. A causa di questo fatto, molte furono le varianti per la scrittura delle frazioni, fino ad arrivare a Diofanto di Alessandria (III–IV sec.) che introdusse un simbolo analogo a quello moderno, anche se i posti di numeratore e denominatore erano tra loro scambiati. Ad esempio, la frazione 2/3 veniva scritta γ/β. Il segno di frazione / detto “virgula” (bastoncello, da “virga”, bastone) non sempre appariva; la frazione veniva infatti anche scritta con i due numeri sovrapposti senza nessun segno di separazione.
Per tutto il periodo greco le frazioni furono sempre usate, ma non furono mai considerate come oggetto specifico di studio, ma piuttosto come strumento di lavoro. A proposito di Diofanto, curioso è il racconto in frazioni della sua vita attribuito a Metrodoro (III sec.), presente nel testo Antologia Palatina: «Questa è la tomba che racchiude Diofanto, meraviglia da completare! Per mezzo dell’arte aritmetica insegna la misura della sua vita. Dio gli concesse la fanciullezza per un sesto della sua vita; dopo un altro dodicesimo la barba coprì le sue guance; dopo un settimo accese la fiaccola nuziale e dopo cinque anni ebbe un figlio. Ahimé! Il misero fanciullo, pur tanto amato, avendo raggiunto appena la metà degli anni di vita del padre, morì. Quattro anni ancora, mitigando il proprio dolore colla scienza dei numeri, visse Diofanto, fino a raggiungere il termine della sua vita». Risolvendo l’equazione contenuta in questo racconto si trova che Diofanto è morto a 84 anni.
La storia delle frazioni ha riguardato anche altre culture come quella indiana, cinese, araba ed è arrivata fino ai giorni nostri con diverse evoluzioni. Tra i contributi indiani ricordiamo il testo scritto nel XII secolo dal matematico Bhaskaracarya, Lilavati, un nome femminile per il quale ci sono diverse interpretazioni. Il libro inizia così: Bella fanciulla dagli occhi lucenti… e continua rivolgendosi spesso a questa fanciulla. Tra gli indovinelli proposti sulle frazioni, citiamo il seguente: uno sciame di api vola sui fiori del giardino; di esse, 1/5 si posa sui gelsomini, 2/3 sui lillà, 1/15 sui gigli mentre due api s’aggirano qua e là senza prendere decisioni… Quante sono in tutte le api dello sciame?
È però nel Liber Abaci di Fibonacci del 1202 che le frazioni, per come le conosciamo noi oggi, appaiono per la prima volta: Fibonacci fornisce le regole delle operazioni sulle frazioni, trova massimi comuni denominatori tra frazioni, trasforma le frazioni in somme di frazioni a numeratore 1 ecc. La cosiddetta “riduzione delle frazioni ai minimi termini” si trova esplicitamente presentata con il nome di “schisare” dai matematici Luca Pacioli (1445-1515) e Nicolò Fontana da Brescia detto Tartaglia (1499-1557). Le parole numeratore e denominatore si affermarono invece nel XV secolo.