Successioni

Una successione è una sequenza ordinata (e spesso infinita) di elementi, come ad esempio numeri, lettere, figure geometriche, giorni della settimana, note musicali, simboli.

Una successione modulare è una successione in cui un gruppo di elementi si ripete senza fine; gli elementi ripetuti costituiscono il modulo della successione. Ad esempio:

▲♣♥▲♣♥▲♣♥▲♣♥▲♣♥▲♣♥▲♣♥▲♣♥▲♣♥ …

è una successione modulare il cui modulo è ▲♣♥, mentre questa

♦♥♥♦♦♥♥♦♦♥♥♦♦♥♥♦♦♥♥♦…

è una successione modulare con modulo ♦♥♥♦. Si può quindi stabilire il modulo e chiedere di creare una successione, viceversa si può fornire una successione e chiedere di individuare il suo modulo.

Una successione per ricorrenza si ha quando ogni termine, escluso il primo che viene definito direttamente, dipende dal termine precedente. Cioè, dopo aver definito il primo elemento della successione, si stabilisce una regola che permette di calcolare il successivo. Prendiamo un numero di partenza, per esempio 1, e poi raddoppiamo sempre; otteniamo:

1          2          4          8          16          32          64          …

Viceversa, se viene data una successione non sempre è facile capire qual è la regola che l’ha generata; per esempio:

1          3          7          15          31          63          127          …

è stata ottenuta partendo da 1, poi raddoppiando e sommando 1.

Invece la seguente:

1          1          1          1          1          1          …

è stata ottenuta partendo da 1 e poi facendo sempre il doppio meno 1; se invece di partire da 1 si fosse partiti da 3, con la stessa regola, avremmo trovato:

3          5          9          17          33          65          …

Occorre inoltre considerare che i primi elementi di una successione possono nascondere più regole, quindi occorre avere l’elasticità di comprendere che quella individuata potrebbe non essere l’unica. Considerando due successioni, queste potrebbero avere i primi elementi in comune, ma in seguito, in base alla regola, potrebbero differenziarsi. Inoltre, ci sono anche successioni casuali, ottenute senza regole (anche se c’è chi dice che la regola ci sia: è quella di aver messo numeri a caso; ma qui si sconfina nella filosofia).

Un’attività che può essere proposta in classe, e che può essere vissuta anche in forma ludica, consiste nel fornire una successione e chiedere qual è la regola o il modulo con la quale si è ottenuta e quali sono gli elementi che permettono di proseguirla. Occorre però stare molto attenti in questi casi perché, come già affermato, non è detto che la regola o il modulo siano unici: più regole o moduli possono dar luogo alla stessa successione o almeno ad una parte di essa.

Ad esempio, questa successione:

♦♥♥♦…

può proseguire in diversi modi:

• usando il modulo ♦♥♥:  ♦♥♥♦♥♥♦♥♥♦♥♥♦♥♥♦♥♥…
• usando il modulo ♦♥♥♦:  ♦♥♥♦♦♥♥♦♦♥♥♦♦♥♥♦♦♥♥♦…
• usando il modulo ♦♥♥♦♣:  ♦♥♥♦♣♦♥♥♦♣♦♥♥♦♣♦♥♥♦♣…
• usando il modulo ♦♥♥♦♣♪♪♣:  ♦♥♥♦♣♪♪♣♦♥♥♦♣♪♪♣♦♥♥♦♣♪♪♣…
• …

Trovare la regola può in certi casi risultare un’attività creativa, stimolante, ma anche complessa, come per la seguente successione:

4     3     3     3     7     6     3     5     4     4     5     6     6     7     …

La successione appare come casuale, eppure non lo è; basta pensare ai nomi dei numeri nella lingua italiana: zero, uno, due, tre ecc. e si scopre che i numeri della successione corrispondono al numero delle lettere dei nomi dei numeri disposti in ordine crescente. Queste proposte possono quindi diventare molto utili per aprire un dibattito in classe costruttivo e interessante. Data una successione si può chiedere agli allievi di trovare una regola; viceversa, data una regola, si può chiedere di continuare una successione di numeri; per rendere ancora più formative e motivanti queste proposte si può chiedere agli allievi di inventare le successioni da sottoporre ai compagni, così da collaborare tra pari.

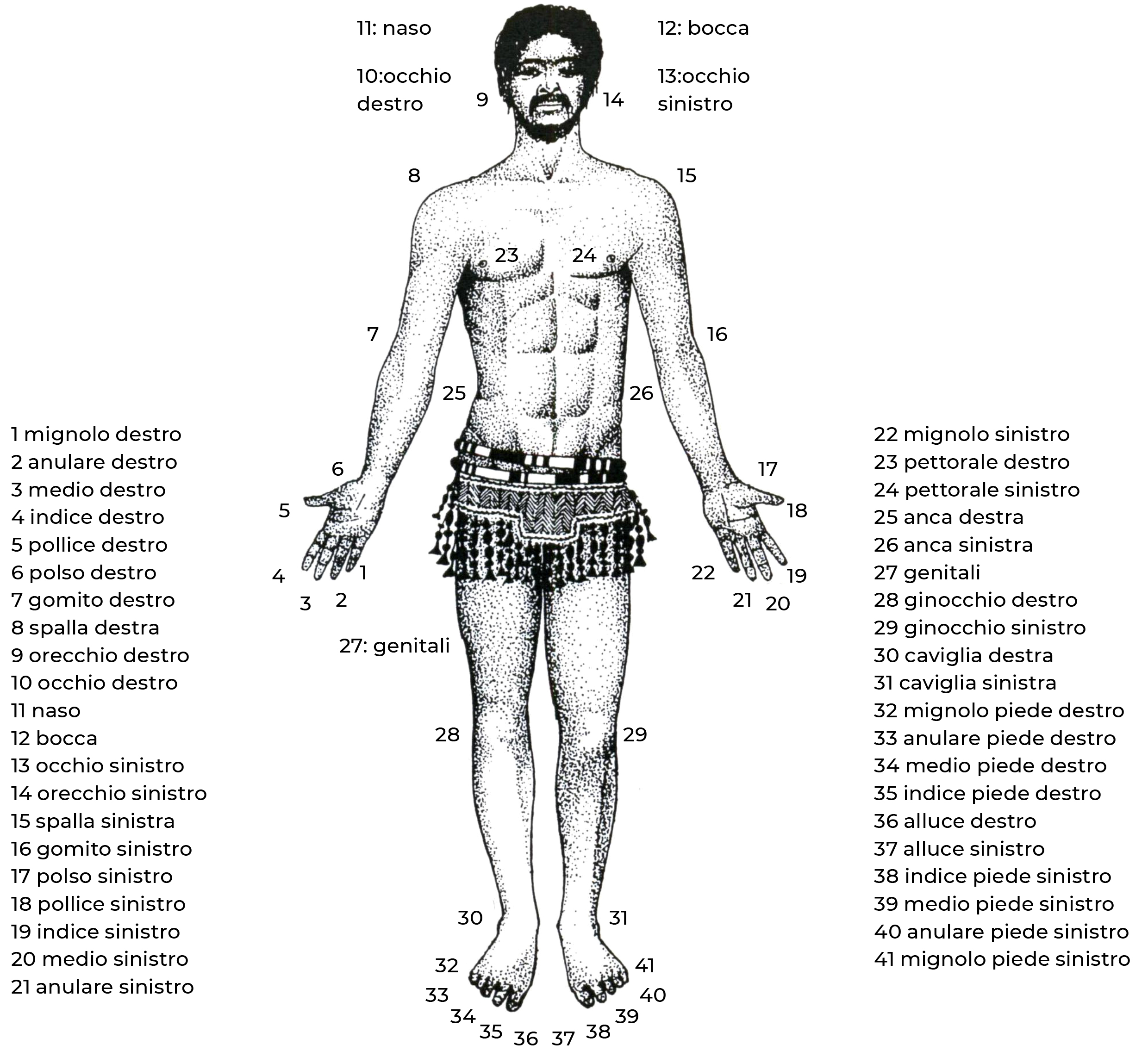
Per riuscire a enumerare, l’uomo si è servito, oltre alle dita delle mani, anche degli arti e delle diverse parti del corpo umano creando una sorta di successione.

I popoli che utilizzavano questo procedimento seguivano un ordine prestabilito, toccandosi in sequenza le diverse parti del corpo. In questo modo potevano elencare una raccolta costituita da un numero di oggetti corrispondenti al numero di riferimenti corporei della successione. Ad esempio, toccandosi il mignolo, l’anulare, il medio, l’indice e il pollice della mano destra, quindi il polso, il gomito, la spalla, l’orecchio e l’occhio dallo stesso lato, si poteva elencare una raccolta costituita da dieci oggetti. Nessuno di tali riferimenti corporei veniva visto come un “numero”; ossia, la semplice designazione di una parte del corpo non bastava a caratterizzare una certa quantità di oggetti se questa non era corredata dalla sequenza data dal toccare le varie parti del corpo.

Con questo procedimento alcune culture arrivavano a contare visivamente fino a 17, altre a 29, alcune a 33 e anche di più. Questo tipo di pratica era assai diffusa nel Medioevo, sia in Europa, sia in Asia, e come riferiscono vari antropologi, i Papua e gli Elema della Nuova Guinea, gli Ingua del Chaco in Paraguay, i Boscimani del Sudafrica e molti aborigeni africani, americani e oceaniani, lo utilizzavano ancora all’inizio del XX secolo.

Tali metodi di enumerazione legati alle parti del corpo erano superiori rispetto a procedimenti elementari come la pratica dell’intaglio o l’accumulo di sassi, perché non utilizzavano solo il principio della corrispondenza biunivoca, ma introducevano anche la nozione di successione, nella quale è implicita la nozione di ordine.

La tecnica evolse nel tempo; successivamente, i popoli cominciarono ad associare le parti del corpo a numeri ben precisi, per cui si ampliò immensamente la possibilità di tenere una contabilità e avviare l’idea di conteggio. Inoltre, grazie al fatto che si considerava sistematicamente la stessa sequenza di parti del corpo per indicare la cardinalità dell’insieme di oggetti da trattare, questa successione diventava, grazie all’abitudine e alla memoria, sempre più astratta, ossia sempre più legata a una successione di numeri.

Una delle successioni più note e famose al mondo è quella inventata dal matematico medievale Leonardo da Pisa (1170-1250), figlio di Bonaccio e perciò chiamato Fibonacci: si parte da un doppio 1 e poi si sommano sempre i due numeri precedenti:

1     1     2     3     5     8     13     21     34     55     89     …

Fibonacci riuscì a individuare tale successione grazie al cosiddetto “problema dei conigli”. In esso si suppone di avere una coppia di conigli (maschio e femmina) neonati; il primo mese la coppia non procrea, perché troppo giovane; ma, a partire dal mese successivo e poi ogni mese, tale coppia genera una nuova coppia (maschio e femmina); questa coppia appena generata non può avere figli nel primo mese, ma poi comincerà a farlo dal secondo mese in poi, generando una nuova coppia (maschio e femmina) ogni mese; e così via. Si domanda quanti conigli si avranno in totale dopo un anno. Questa situazione resta definita appunto dalla successione di Fibonacci: 1 (1 coppia all’inizio), 1 (ancora 1 sola coppia dopo un mese), 2 (2 coppie dopo due mesi), 3 (3 coppie dopo tre mesi), 5 (5 coppie dopo quattro mesi), 8, 13, 21, 34, 55, 89, 144, 233 (233 coppie dopo un anno). Ovviamente si può proseguire oltre: 377 coppie dopo il tredicesimo mese e così via.

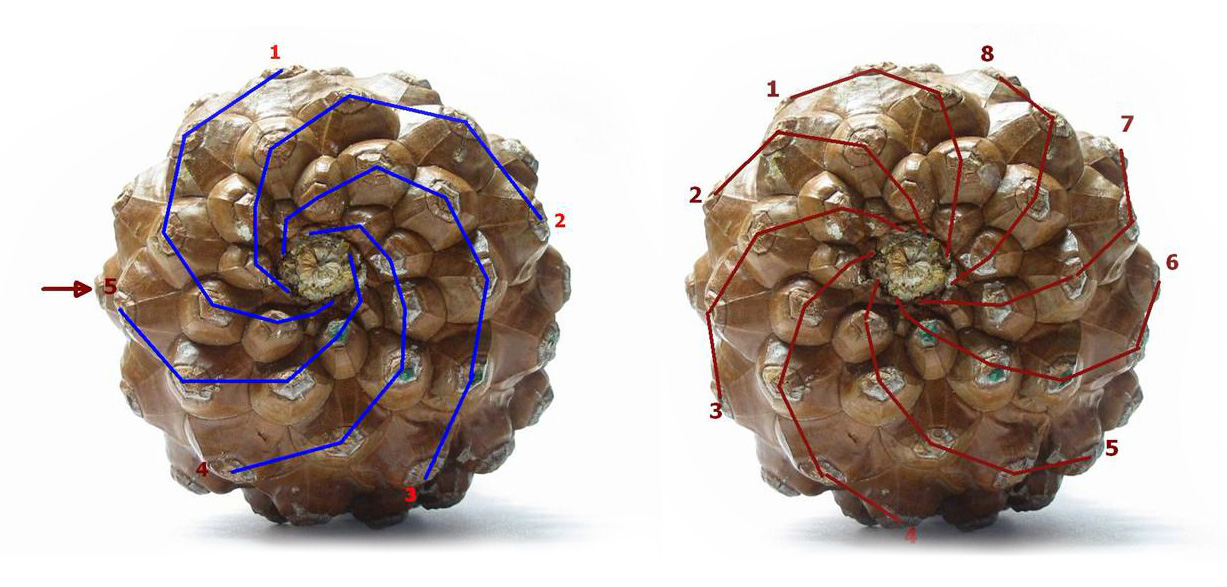
Questa straordinaria successione, ricca di proprietà, è molto presente in natura, in forme viventi e non viventi; per esempio, si ritrovano i numeri della successione nel numero di spirali di semi nella corolla di un girasole, di spirali di un ananas o di una pigna, nella struttura di un cavolfiore o della conchiglia del Nautilus. Dal punto di vista matematico va osservato che, calcolando i rapporti tra due numeri successivi della successione di Fibonacci, si trovavano valori sempre più vicini all’affascinante numero aureo o numero φ di Fidia, 1,618033988…, canone di bellezza e armonia. Ecco i rapporti tra due numeri successivi della successione di Fibonacci tendente al numero aureo:

La natura sembra cioè comportarsi matematicamente in modo additivo, secondo la successione di Fibonacci, e il suo “tendere” è aureo.