Pari e dispari

Come si fa a distinguere i pari dai dispari? Ebbene, basta dividerli per 2. Se l’operazione ha resto 0, il numero è pari; se l’operazione ha resto 1, il numero è dispari.

Un numero è quindi pari se è divisibile per 2, in caso contrario è dispari.

Il più piccolo numero pari è quindi 0, essendo 0 divisibile per 2, dato che 0 : 2 fa 0 e il resto è 0.

Possiamo notare che i numeri naturali partono da 0, pari, e poi proseguono alternativamente con un dispari, un pari, un dispari, un pari e così via.

Ma se si ha un numero grande come 276'845'425, come si può stabilire se è pari o dispari senza fare una impegnativa divisione? Per decidere se quel numero è divisibile per 2, è sufficiente considerare solo l’ultima cifra, nel nostro caso solo il 5: poiché quest’ultima cifra è dispari, sarà dispari anche l’intero numero; questa verifica è più che sufficiente per stabilire la divisibilità per 2 di un numero.

Chiediamoci se ci sono più numeri nell’insieme dei numeri naturali ℕ o nell’insieme dei numeri pari P.

A prima vista, si potrebbe pensare che in ℕ ci sono più elementi che in P, dato che in ℕ ci sono tutti i pari, ma anche tutti i dispari. Il ragionamento è legittimo, e appare corretto, ma ricordiamo che abbiamo a che fare con l’infinito, e tutto quel che siamo abituati a pensare sulle raccolte finite non è detto che valga per le raccolte infinite.

Per l’infinito, infatti, non è sempre vero che “il tutto è maggiore della sua parte”. Basta procedere con il metodo delle corrispondenze biunivoche per scoprire che ci sono tanti numeri naturali quanti numeri pari, ossia ℕ e P hanno la stessa quantità di elementi.

Scriviamo idealmente tutti i numeri naturali in una riga e, sotto, tutti i numeri pari:

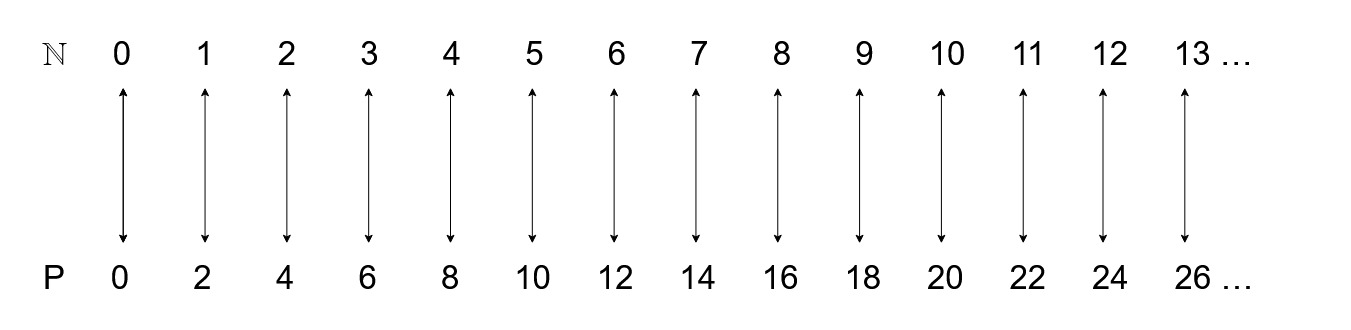
Che cosa si nota? Che ad ogni numero naturale corrisponde un ben preciso numero pari, il suo doppio; o viceversa, a ogni numero pari corrisponde un ben preciso numero naturale, la sua metà. Dunque: si può creare una corrispondenza biunivoca tra gli elementi di ℕ e di P, e possiamo così concludere, a sorpresa, che ci sono tanti numeri naturali quanti numeri pari.

L’infinità dei numeri naturali si chiama: “infinità del numerabile”.

Corrispondenze biunivoche possono essere trovate anche tra numeri naturali e dispari, tra naturali e numeri quadrati {1, 4, 9, 16, 25, 36, 49, …}, tra naturali e multipli di un numero ecc. Dunque, i numeri naturali e un qualsiasi sottoinsieme di ℕ costituito da infiniti elementi posseggono lo stesso tipo di infinità del numerabile.

La corrispondenza biunivoca tra i numeri naturali ℕ e i numeri quadrati è stata messa in evidenza da Galileo Galilei (1564-1642) e fu detta paradosso di Galilei (si veda il contenuto Corrispondenza biunivoca).

Le occasioni per far emergere la differenza tra numeri pari e dispari non mancano nella quotidianità della vita di classe, ad esempio quando è necessario disporsi in fila per due per uscire dall’aula, quando devono formarsi due squadre con lo stesso numero di giocatori ecc. I bambini spesso si accorgono da soli che in alcuni casi è possibile dividersi a metà, mentre a volte “avanza un compagno” o “serve un compagno in più”.

Queste osservazioni spontanee possono essere formalizzate nei primi due anni di scuola elementare introducendo i numeri pari e i numeri dispari prevalentemente come alternanza dei numeri, senza dimenticare lo zero, che rappresenta il più piccolo numero naturale pari. Per far intuire agli allievi la differenza tra questi due insiemi numerici può essere approcciata già nel primo ciclo la divisibilità dei numeri per 2, ma questo aspetto deve poi essere consolidato e formalizzato nel ciclo successivo, tramite il concetto di divisibilità. In entrambi i cicli è possibile proporre giochi e attività che vertono su questi insiemi e nel secondo ciclo è importante far intuire agli allievi che vi sono tanti numeri naturali quanti numeri pari o dispari.