Grafici e tabelle

I grafici e le tabelle sono delle rappresentazioni di dati, espressi in varie forme (numerica, a parole ecc.), che hanno lo scopo di renderli facilmente consultabili e interpretabili. Le tipologie di grafici e tabelle sono varie e si differenziano in base al metodo di rappresentazione e allo scopo specifico per cui vengono usate. Una rappresentazione può essere quindi più o meno funzionale a seconda dello scopo.

Una tabella è un importante e diffuso strumento utile per organizzare dati e rappresentare relazioni, che vengono riportati nelle celle di intersezione tra le colonne verticali e le righe orizzontali (che possono essere identificate con un nome).

Una particolare tabella è il diagramma di Carroll, dal nome di Lewis Carroll (1832-1898), che consiste in una rappresentazione a due vie, del tipo sì / no o vero / falso.

Una tabella a doppia entrata fornisce un’efficace visualizzazione degli insiemi su cui si considera la relazione, e delle caratteristiche delle coppie di elementi in relazione (gli incroci); questa rappresentazione può risultare efficace quando non è importante l’ordine tra gli insiemi.

Il diagramma sagittale o a frecce, invece, è una rappresentazione che permette di visualizzare tramite collegamenti grafici, come le frecce, le relazioni che sussistono tra elementi di due insiemi.

L’ideogramma è una modalità di rappresentazione che usa immagini che evocano il fenomeno o la variabile considerata. È costituito da più simboli uguali ognuno dei quali indica un certo numero di elementi. Tale rappresentazione è molto usata nei quotidiani, in quanto fornisce informazioni di immediata lettura dei dati, soprattutto in termini di confronto, anche se potrebbero risultare piuttosto approssimative.

I grafici a barre, come ad esempio i grafici a colonne e a nastri (quando i rettangoli sono disposti in orizzontale), sono costituiti da tanti rettangoli quante sono le modalità da rappresentare, che vengono posizionati su un’asse di riferimento orizzontale (o rispettivamente verticale) e sono separati tra loro. La lunghezza dei lati dei rettangoli che si trovano sull’asse è fissa per ciascun rettangolo e scelta liberamente, mentre l’altezza è proporzionale alla frequenza o all’intensità che rappresentano.

I grafici a barre sono assai diversi dagli areogrammi e dagli istogrammi, in quanto in questi ultimi casi la frequenza corrisponde all’area delle figure rappresentate di solito rispettivamente con settori circolari o con rettangoli.

L’areogramma è un tipo di rappresentazione grafica in cui i dati vengono visualizzati tramite una figura geometrica piana o tridimensionale, suddivisa in regioni le cui aree sono proporzionali ai vari dati a cui si riferiscono. Il numero di dati è spesso espresso in percentuale, ma può anche essere espresso in forma numerica. Questo tipo di rappresentazione è particolarmente adatto per operare confronti fra diverse grandezze, senza necessariamente riferirsi a un totale.

Quando è importante evidenziare il riferimento a un totale si usa un particolare tipo di areogramma detto diagramma a torta o circolare, nel quale le varie frequenze percentuali o relative sono raffigurate da ampiezze di angoli di settori circolari che dividono un cerchio. In questo modo l’area di ogni settore circolare risulta proporzionale alla percentuale rappresentata.

Si parla invece di istogramma se i dati numerici vengono rappresentati tramite aree di rettangoli, adiacenti tra loro e allineati su un asse orientato, dotato di unità di misura. Ogni rettangolo ha il lato sull’asse orientato di lunghezza pari all’ampiezza della corrispondente classe e l’altezza che rappresenta la densità di frequenza, ossia il rapporto fra la frequenza (assoluta) associata alla classe e l’ampiezza della classe. L’area della superficie di ogni rettangolo coincide con la frequenza associata alla classe cui il rettangolo si riferisce; per tale caratteristica gli istogrammi rappresentano un tipo di areogramma.

Forse i grafici più conosciuti sono i diagrammi a due variabili (x, y) (più raramente a tre) per rappresentare relazioni tra insiemi numerici, che si basano prevalentemente sul concetto di piano cartesiano. Tale piano è costituito dall’asse delle ascisse che rappresenta una retta di riferimento (solitamente caratterizzata dalla lettera x), dall’asse delle ordinate, che costituisce una retta ortogonale alla precedente (solitamente caratterizzata dalla lettera y) e dall’origine, il punto nel quale si incontrano le due rette. Tramite questi elementi è possibile individuare ogni punto del piano con una coppia di numeri reali chiamati rispettivamente ascissa e ordinata del punto, i cui valori assoluti rappresentano le distanze del punto rispettivamente dall’asse x (ascissa) e dall’asse y (ordinata). Determinati i punti sul grafico grazie alle due variabili, è possibile unirli se si vuole rappresentare un andamento. Se l’andamento è temporale, per convenzione, si rappresenta lo scorrere del tempo sull’asse orizzontale (x).

Fin dai primi anni di vita, i bambini iniziano a indagare e a interpretare il mondo e la realtà che li circonda e sentono il bisogno di tradurlo, capirlo e spiegarlo ricorrendo alle prime forme di rappresentazione, mentali e scritte.

L’atto del rappresentare sembrerebbe quindi essere un bisogno naturale presente già nei più piccoli, che nasce anche dalla voglia di comunicare. La rappresentazione viene prodotta dalla mente di ciascun individuo, ma necessita di dati provenienti dall’esperienza. È quindi necessario che a scuola i bambini possano sperimentare e provare, venendo inseriti in contesti e situazioni che richiedono la realizzazione, l’utilizzo, l’interpretazione e la lettura di diverse rappresentazioni che coinvolgano dei dati.

È importante lasciare che gli allievi si esprimano inizialmente liberamente attraverso rappresentazioni spontanee (come disegni, parole e grafici) che si arricchiranno grazie al confronto con quelle degli altri.

Tra le rappresentazioni spontanee di quantità numeriche rilevate dalla vita di classe, come ad esempio la registrazione dei giorni di sole, di pioggia o i giorni nuvolosi che si rilevano in un mese, emergono fin dalla prima elementare i primi spontanei esempi di tabelle, di diagrammi a frecce, di grafici a barre, in alcuni casi anche di areogrammi. Tali rappresentazioni si possono realizzare inizialmente con materiali concreti come scatole, lego, cubetti, per poi passare alla rappresentazione su carta. L’esigenza di voler rappresentare può nascere dal bisogno di comunicare i dati da loro reperiti a vari interlocutori, come compagni di scuola, familiari, oppure un personaggio fantastico. È importante poi riflettere con i bambini su vantaggi e svantaggi delle varie rappresentazioni scelte e come questi variano in base ai diversi contesti. Nel primo ciclo è interessante anche far confrontare gli allievi con vari tipi di grafici e tabelle proposti dal docente in cui si riassumono informazioni o con cui si effettuano giochi, come ad esempio le varie rappresentazioni dei diversi tipi di calendari per la settimana, il mese o l’anno, che ampliano e rafforzano ulteriormente il loro bagaglio di esperienze. Tali rappresentazioni possono essere anche vissute in prima persona con il corpo, come è il caso del gioco del twister o di battaglia navale, che favorisce un primo approccio al piano cartesiano, per poi passare a vivere il microspazio del foglio di carta.

Tra le varie proposte che si riscontrano nella pratica vi è quella di contare raccolte di oggetti e di registrarne il numero. Da questo punto di vista occorre fare attenzione, perché se si vuole lavorare sul numero di elementi e sul confronto di numerosità, non bisogna inizialmente rafforzare la misconcezione che ci sia una dipendenza tra la numerosità e la misura della rappresentazione (la colonna più “alta” sarà sicuramente la più numerosa), perché questa dipendenza nella realtà non sempre si verifica: la numerosità di raccolte di oggetti non dipende infatti dalla loro grandezza. Rappresentazioni iniziali del tipo: a zero corrisponde il niente; all’uno, un quadratino; a due, due quadratini congruenti sovrapposti; a tre, tre quadratini congruenti sovrapposti ecc., proposte troppo presto, possono generare convinzioni erronee come a metrica è associata quantità. In effetti, una cosa è la lettura di un grafico a barre da parte di un bambino che ha già imparato a contare gli oggetti indipendentemente dalla loro grandezza, altra cosa è l’immagine che si fa chi deve ancora apprendere tali concetti; se l’obiettivo è far capire agli allievi il concetto di numero, sicuramente i grafici a barre non aiutano la formazione di tale sapere. Didatticamente converrebbe far contare insiemi formati da oggetti di tipologia e dimensioni diverse, far costruite grafici spontanei eventualmente costruiti con oggetti diversi come forma e dimensione, per fare così intuire che la numerosità non dipende dalla metrica degli oggetti. Successivamente, quando il concetto di numero si sarà formato nella mente degli allievi, si potranno proporre situazioni legate al vissuto rappresentate poi con grafici a barre convenzionali.

Nel secondo ciclo è inoltre possibile approfondire in modo sempre più consapevole la raccolta e il trattamento dei dati. Prima di tutto occorre stabilire il problema che si vuole studiare, ossia che cosa si vuol conoscere con l’indagine, e le modalità di rilevazione, ovvero quali e quanti dati si vogliono o possono raccogliere e in che modo viene effettuata.

I problemi possono scaturire da diversi contesti vicini al vissuto degli allievi (provenienza geografica o sport praticati degli allievi della scuola, altezza media o altre caratteristiche degli allievi ecc.) e possono essere rappresentati tramite grafici o tabelle, cercando di considerare criticamente i diversi tipi di rappresentazione possibili per poi individuare quello più efficace per lo scopo comunicativo che ci si è prefissati. Tra questi tipi, si può far uso anche di quelli convenzionali.

Ciò che importa non è certamente il nome delle diverse tipologie di grafici e tabelle, ma il saperle creare, leggere e interpretare, che costituisce una delle competenze fondamentali per il futuro cittadino.

Nel terzo ciclo della scuola dell’obbligo tale competenza rientrerà nell’ambito Funzioni.

L’esigenza di leggere, interpretare e rappresentare il mondo è sempre stata una costante dell’essere umano.

Fin dall’antichità, in diverse civiltà, come quella mesopotamica, nell’antico Egitto, nel popolo ebraico, nell’antica Roma, l’uomo ha raccolto informazioni relative alla popolazione per fini fiscali o militari. La raccolta di questi dati veniva rappresentata principalmente sotto forma di lunghe tabelle.

Invece, per quanto concerne la storia dei grafici maggiormente usati oggi per la lettura di dati, un periodo fondamentale è stato quello tra il XVI e il XVII secolo, detto dell’algebra simbolica, che si è sviluppato grazie soprattutto all’opera dei francesi François Viète e René Descartes (Cartesio).

È a Cartesio che si deve la nascita nel 1637 del sistema di riferimento, detto appunto cartesiano, che identifica una specifica posizione di un punto o di un oggetto su una superficie. Grazie a Cartesio fu così introdotto quell’importante legame tra algebra e geometria, in un metodo che viene ancora oggi riconosciuto e denominato “geometria analitica” e che fu in seguito sviluppato e perfezionato da altri matematici, primo fra tutti Pierre de Fermat. L’importanza del lavoro di Cartesio sta nel metodo individuato, che ha come scopo la creazione, tramite la matematica, di uno strumento per descrivere la realtà delle scienze naturali, in particolare della fisica e della meccanica; la matematica venne così ad assumere un ruolo di primissimo piano, per le impareggiabili potenzialità di oggettività e di rigore che sono state poi applicate in tutti i campi del sapere attuali.

Tra il XVII e il XVIII secolo aumentò anche l’interesse per la raccolta di numeri che descrivevano la situazione dei vari paesi del mondo, così da aiutare a prendere decisioni economiche e sociali sulla base della previsione di determinati fenomeni. In questo periodo prese forma la moderna statistica, una scienza matematica in grado di raccogliere e interpretare i dati, in modo da studiare fenomeni collettivi di qualsiasi tipo.

Con il progredire dello studio di questa disciplina, nacque anche l’esigenza di rappresentare i dati in modo che potessero essere facilmente leggibili e interpretabili. È nel 1800 che si iniziò a pensare a organizzare i dati creando areogrammi, istogrammi, ideogrammi ecc., visto che la rappresentazione in tabella non era sempre quella più efficace.

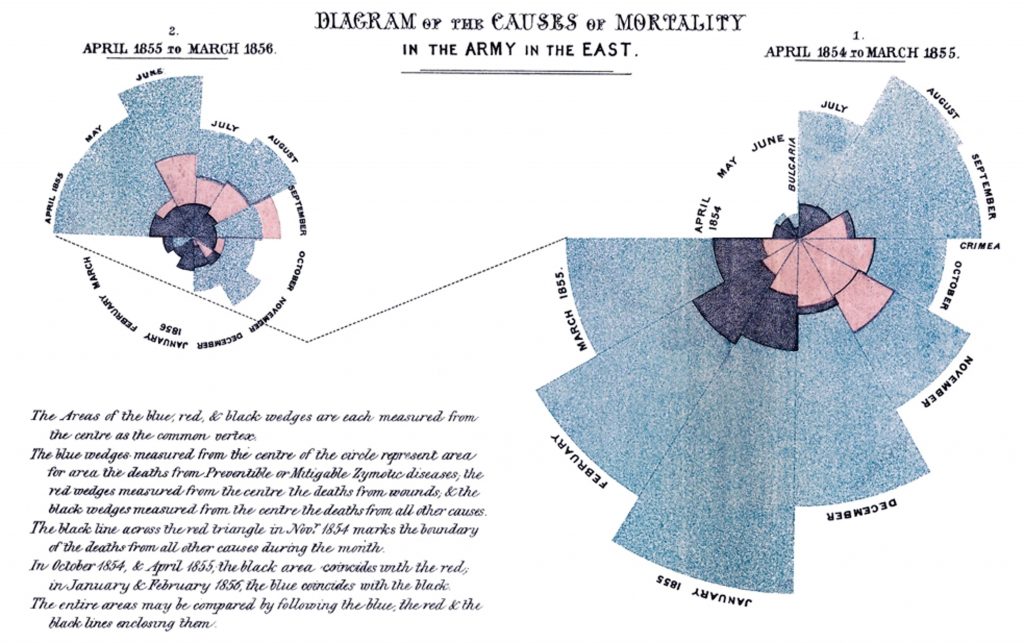
Un aneddoto interessante è quello dell’infermiera Florence Nightingale (1820-1910), nata da una famiglia benestante inglese, che convinse i genitori a ricevere un’istruzione matematica, anche se loro non la ritenevano una materia “adatta alle donne”. Interessata ai problemi sociali dell’epoca, inizia a lavorare come infermiera e a studiare il funzionamento e l’organizzazione degli ospedali dell’epoca e, durante la guerra di Crimea ha l’occasione di raccogliere informazioni sui soldati feriti e sulle loro cause di morte. Decide poi di rappresentare i dati raccolti in grafici, che lei chiama coxcombs, che rappresentano i predecessori dei moderni areogrammi. Grazie a questi suoi studi riesce a stabilire che i soldati hanno più probabilità di morire per una malattia non curata che per una ferita riportata in battaglia e a dimostrare che migliorando le condizioni sanitarie degli ospedali si poteva ridurre il tasso di mortalità dei pazienti. È considerata la fondatrice dell’infermieristica moderna, grazie al suo contributo nella riforma del sistema sanitario e ai numerosi libri e manuali che scrisse per trasmettere le sue idee e conoscenze sul mestiere di infermiere; è inoltre anche la prima donna ad essere stata ammessa alla Royal Statistical Society, importante istituzione per la statistica britannica e mondiale.

Grazie alla tecnologia, oggi è molto più agevole ed efficace raccogliere ed elaborare dati. Uno dei settori oggi in grande espansione è proprio quello dell’analisi dei dati: le persone che lavorano in questo campo sono dette data analyst. Un data analyst, oltre ad avere competenze in matematica e in informatica, deve avere anche buone abilità di comunicazione per poter spiegare e diffondere i risultati delle sue analisi. Per questo è molto importante scegliere la rappresentazione migliore dei dati raccolti, così da rendere chiari i risultati delle proprie ricerche a tutti. Ci sono persone specializzate solo in questo specifico campo, detto data visualisation.