Strategie di calcolo

Il calcolo è un argomento centrale dell’apprendimento matematico, che risulta funzionale a tutti gli ambiti della disciplina e a tutte le diverse aree culturali. Può essere considerato come un processo mentale che trasforma più dati in ingresso in uno o più risultati. Il termine calcolo ha assunto oggi diversi significati anche assai distanti rispetto a quello classico di “calcolo aritmetico” (si parla ad esempio di “calcolo della probabilità” o di “calcolo di una strategia”).

Lo stesso calcolo aritmetico, basato prevalentemente su algoritmi definiti, a volte concepiti come univoci, nel tempo ha cambiato significato, assumendo oggi una connotazione più strategica e ampia. Ciò è principalmente dipeso dalla diffusione generalizzata dei più svariati mezzi tecnologici, che ne ha influenzato il ruolo e le caratteristiche, e dall’importanza che assume attualmente la risoluzione di problemi nella formazione del futuro cittadino.

Il calcolo aritmetico trova infatti oggi la sua principale ragione d’essere nei processi risolutivi di situazioni-problema nel cui contesto va opportunamente affrontato, sviluppato ed esercitato. Questo non toglie che risulta ancora oggi fondamentale nella scuola elementare saper gestire calcoli aritmetici, non affrontati in modo meccanico e acritico e basati esclusivamente su algoritmi tradizionali, bensì concepiti in modo più ampio e consapevole.

È infatti importante saper gestire calcoli prevalentemente mentali, basati su strategie personali che tengano conto delle proprietà dei numeri e delle operazioni, e che non portino solo ad un risultato esatto, ma che coinvolgano anche stime e approssimazioni legate ad apprendimenti superiori, come l’analisi e la sintesi, l’intuizione e l’invenzione. Si tratta dunque di un approccio strategico del calcolo mentale che rafforza la padronanza del valore posizionale delle cifre, alimentando il senso del numero, della stima e del controllo delle soluzioni.

La stima computazionale, legata ai risultati di un calcolo, si basa sul saper trasformare con consapevolezza i numeri o un problema, dalla sua forma originale a una nuova forma che dia approssimativamente una risposta equivalente e che sia facilmente risolvibile mediante calcolo mentale. È proprio il processo di semplificazione dei numeri o del problema, sui quali si innesta poi il calcolo mentale, che porta ad ottenere risultati approssimati e non esatti: per questo, talvolta, si usa l’espressione calcolo mentale approssimato in riferimento alla stima computazionale.

All’ingresso della scuola elementare i bambini hanno già alcune concezioni relative a calcoli di tipo additivo basate su strategie di conteggio che iniziano a padroneggiare tramite l’uso delle dita delle mani, manipolate in modi assai diversificati e personali, spesso accompagnate da forme verbali. Su queste concezioni spontanee va costruito l’apprendimento, senza imporre troppo presto eccessivi formalismi, i quali si basano soprattutto su convenzioni di scrittura e meccanismi univoci. È poi grazie alla condivisione di diverse strategie utilizzate dai vari allievi per effettuare un calcolo, e dalla valutazione dei punti di forza e di debolezza di ciascuna, che è possibile farle evolvere. È importante osservare che la condivisione porta a una pluralità di strategie che possono anche coesistere per più tempo. In questa evoluzione, poi, risulta importante mostrare analogie e differenze tra tipologie di calcoli per riconoscerne elementi comuni e generalizzabili. Si passerà in seguito a calcoli che coinvolgono anche le altre operazioni. I tipici apprendimenti funzionali alle strategie di calcolo, come individuare gli addendi che sommati danno il 10, apprendere in maniera sicura le caselline/tabelline relative alla moltiplicazione, risultano ancora oggi importanti per favorire un approccio più efficiente del calcolo a mente.

Risulta però importante distinguere ciò che deve essere appreso in modo automatico (come i due addendi che danno il 10, le caselline/tabelline entro il 10), così da poter abbandonare le lente procedure di conteggio, da ciò che deve rimanere ragionato, ossia basato sul cosiddetto calcolo pensato o cosciente.

Anche gli algoritmi tradizionali di calcolo possono essere mostrati per comprenderne il funzionamento, mettendoli eventualmente a confronto con altri in uso in differenti culture o in diversi momenti storici, ma ciò che va privilegiato è il calcolo mentale, ossia quello ragionato. Gli algoritmi possono anche essere eseguiti con carta e penna, ma – a differenza del calcolo scritto tradizionale in colonna – si può svolgere il calcolo in riga o comunque secondo algoritmi “spontanei”.

Gli algoritmi scelti non sempre devono portare a un calcolo esatto, ma occorre anche richiedere la stima del risultato di un calcolo, prevedendone l’ordine di grandezza o un risultato approssimato. Va considerato che le diverse strategie di calcolo, sia scritto sia mentale, vertono prevalentemente sulle proprietà dei numeri e delle operazioni, che devono essere comprese, gestiste e utilizzate in modo strategico dagli allievi.

Alla fine del secondo ciclo la stima può essere anche accompagnata da un uso sensato ed efficace della calcolatrice, così da valutare l’attendibilità della stima effettuata; tale strumento può essere introdotto mostrandone benefici e limiti, anche attraverso vere e proprie sfide tra calcolo mentale gestito dagli allievi e calcolatrice, così da sviluppare anche senso critico nei confronti delle tecnologie. La calcolatrice o altri mezzi informatici possono costituire utili strumenti da usare per eseguire calcoli di una certa complessità, in situazioni in cui occorre lavorare sui risultati in modo sperimentale o in cui è importante puntare sul processo risolutivo di una situazione-problema e non sui singoli calcoli. Nella risoluzione di problemi, i processi di stima e controllo dei risultati possono educare gli allievi a non trascurare le importanti fasi di interpretazione e validazione dei risultati nel ciclo della matematizzazione (ciclo messo in evidenza dalla valutazione standardizzata internazionale PISA e che riassume i processi di risoluzione dei problemi), che vengono messi in campo nella delicata fase di ritorno dalla soluzione matematica al problema reale di partenza. Inoltre, il calcolo mentale e la stima favoriscono una particolare attenzione al procedimento risolutivo, piuttosto che al prodotto finale, promuovendo la ricerca di molteplici strategie personali. La stima, infine, coinvolge importanti fattori piscologici-affettivi quali la confidenza nelle proprie capacità e la tolleranza all’errore.

Lo scopo è di sviluppare una competenza nell’affrontare e risolvere situazioni problema riconducibili alle quattro operazioni, fondata sul possesso di un bagaglio tecnico-algoritmico utile nella vita quotidiana che permetta di trovare delle soluzioni, di presentare e giustificare i procedimenti messi in atto, di giudicarne l’attendibilità, procedendo anche per tentativi nel caso di situazioni poco familiari.

Il calcolo ha origini storiche molte antiche, legate all’uso delle dita delle mani, delle parti del corpo e di oggetti concreti come sassolini, conchiglie, bastoncini di legno, oggetti d’argilla, che sono presenti nelle diverse epoche e nelle diverse culture.

La mancanza di un sistema posizionale in culture come quella Greca, Etrusca, Latina e Romana rendeva impossibile l’uso di algoritmi per come li intendiamo noi oggi e dunque fiorirono e si diffusero vere e proprie macchine da calcolo, dette abachi. Ad esempio, la tavola di Salamina ha rappresentato un formidabile strumento di calcolo aritmetico diffuso nel mondo greco soprattutto nell’epoca compresa tra il VI e il V secolo a. C.

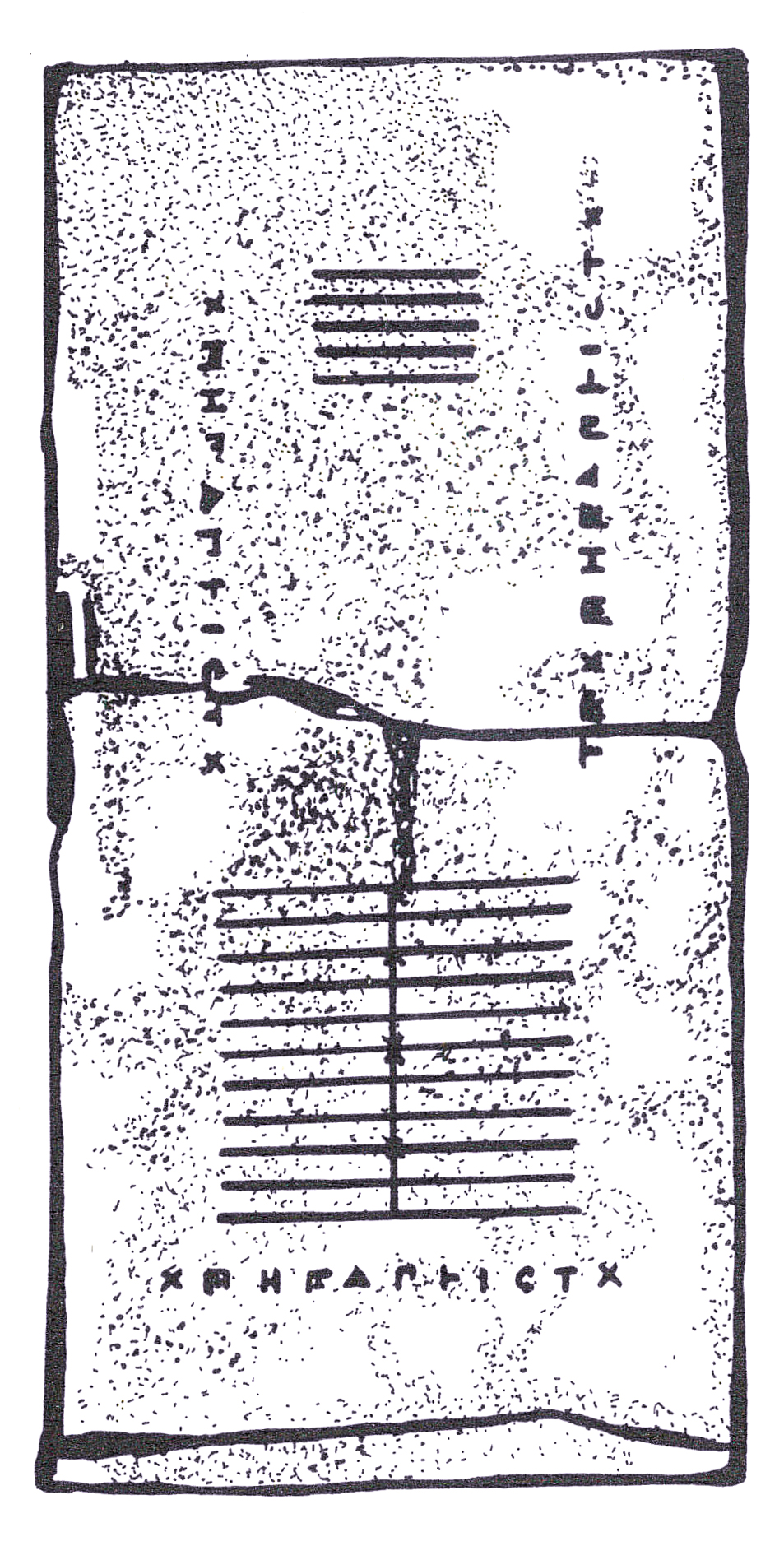
Questo strumento di calcolo non è molto diverso da quelli usati successivamente dai contabili medievali in Europa e forse apparteneva dunque a qualche addetto alla riscossione dei tributi o, più probabilmente, era stata usata in qualche scuola per contabili.

Nelle scanalature si ponevano e poi si facevano scorrere palline o sassolini, in latino calculi, da cui l’odierno nome italiano calcolo e il verbo calcolare.

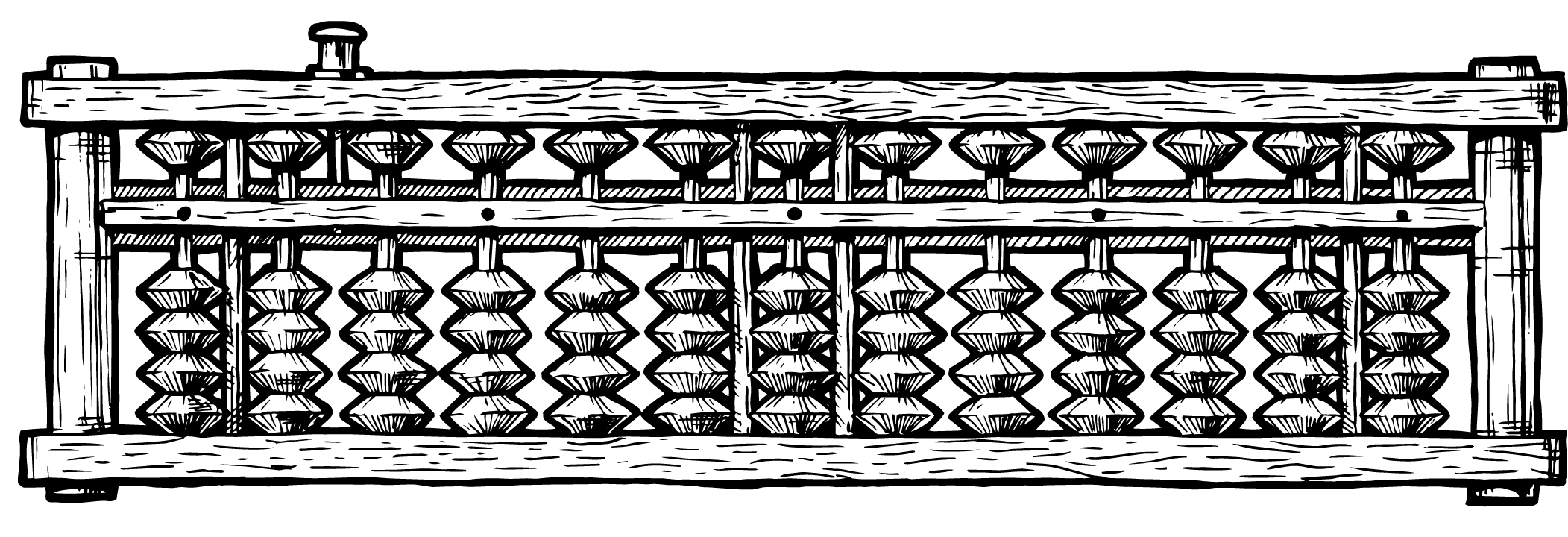
Ma l’abaco non fu inventato solo alle nostre latitudini, nell’oriente l’abaco ha origini ancora più antiche ed è ancora utilizzato; in Cina è attualmente conosciuto con il nome suan-pan, in Giappone con il nome di soroban. Il soroban risultava sicuramente lo strumento di calcolo aritmetico più veloce prima della diffusione delle calcolatrici elettroniche e in un certo senso, per un certo periodo, anche dopo.

Anche gli Aztechi e gli Inca avevano creato degli abachi e così fecero le culture a essi collegate. Una delle macchine di calcolo incaiche più famose è la yupana, una scacchiera tuttora in uso soprattutto per motivi didattici in alcuni paesi dell’America Meridionale. Un altro strumento servito non solo a memorizzare o rappresentare numeri, come si credeva all’inizio, ma anche a eseguire calcoli, è il quipu, che vuol dire nodo.

Un’evoluzione del quipu, tuttora in uso presso alcune popolazioni autoctone della Bolivia e del Perù, è il chimpu. In questo caso le cordicelle del quipu sono sostituite con un fascio di sottili cordicelle che mostrano con maggiore chiarezza l’ordine decimale corrispondente: 3 nodi su una sola cordicella del fascio indicano 3 unità, 3 nodi su due cordicelle simboleggiano invece 3 decine, 5 nodi su tre cordicelle rappresentano 5 centinaia e così via.

Uno degli abachi più diffusi nell’Europa occidentale, dalla penisola iberica alla Germania, era l’abaco a righe medievale.

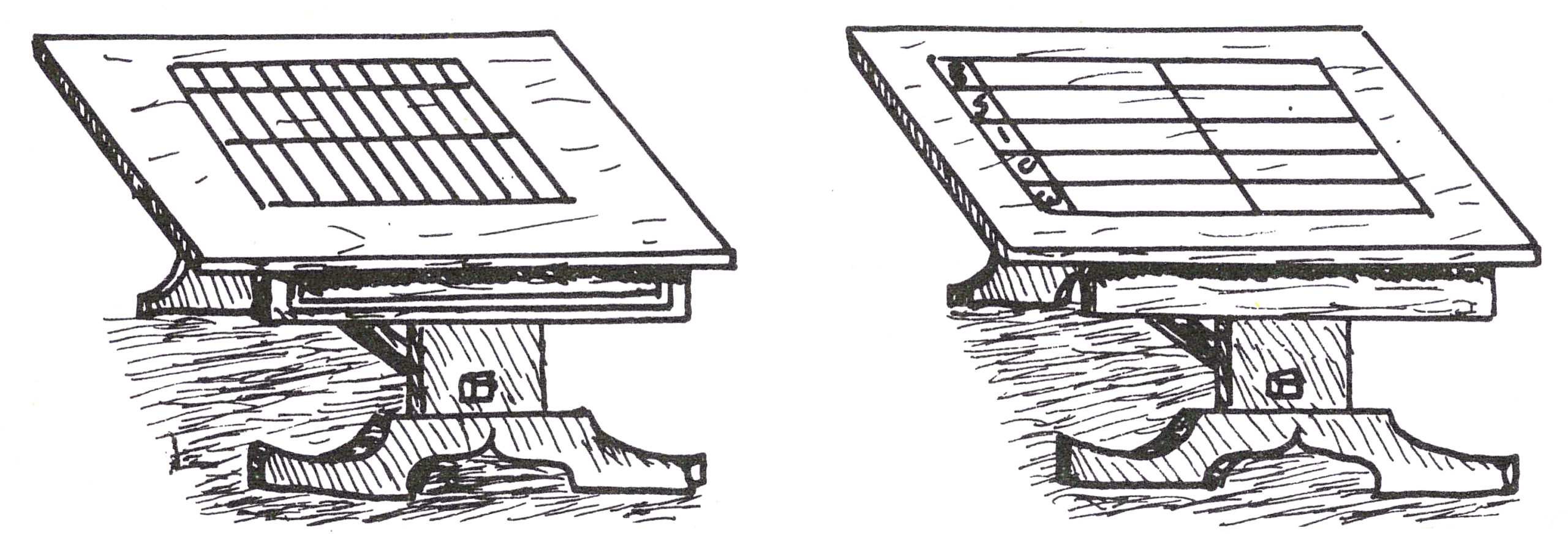
Si tratta di una tavola orizzontale sulla quale vi sono righe parallele, orizzontali e verticali, che formano regioni rettangolari ciascuna delle quali indica un diverso ordine decimale, la prima in basso indica le unità e così di seguito verso l’alto. Sulle righe si dispongono gettoni il cui valore dipende dalla posizione; ma si possono anche porre gettoni tra una riga e l’altra per indicare 5 (tra la prima e la seconda, unità e decine), 50 (tra la seconda e la terza, decine e centinaia) e così via. Così facendo su una stessa riga vi sono al massimo 4 gettoni e tra l’una e l’altra al massimo uno. Siccome con questo strumento si raggiungevano cifre enormi (per l’epoca) ci si serviva di crocette per separare le cifre fino a 999, poi le migliaia, i milioni, come si fa ancora oggi con i puntini; ad esempio 3⁺245⁺765, che oggi si scriverebbe 3˙245˙765.

I vari tipi di abaco adottati avrebbero potuto dunque indurre i contabili a sfruttare il principio posizionale per scrivere i numeri, già diffuso nel mondo islamico, ma ancora non presente in quello cristiano; ciò avrebbe consentito così di sfruttare i metodi algoritmici arabi, rapidi ed efficaci. Ma i contabili di scuola abacista non accettarono per vari secoli questa idea che a noi sembra oggi così naturale. Il nostro attuale agevole sistema di numerazione posizionale fu ideato nell’India del Nord attorno al V secolo, si diffuse nel mondo arabo e infine entrò nel bacino del Mediterraneo e in Europa.

Vari autori di diversa estrazione sociale e culturale contribuirono a diffondere in Europa le nuove idee sul calcolo aritmetico provenienti dall’India e dal mondo arabo. Tra questi il più noto è il mercante italiano Fibonacci, che nel 1202 presentò un’opera manoscritta formata da quindici capitoli dal titolo Liber Abaci, ossia Libro dell’abaco, libro del calcolo, diventato un classico, celebre in tutto il mondo. In questo libro non si parla dell’abaco come strumento, bensì delle nove “cifre” indiane (le figure delli Indi), del “segno” zero della numerazione indiana, dei nuovi algoritmi e di vari problemi famosi (ad esempio, il problema dei conigli che ha dato origine alla famosa “successione di Fibonacci”). Il Liber Abaci di Fibonacci costituisce il primo contributo alla diffusione in Occidente di modalità di calcolo più funzionali rispetto a quelle che tradizionalmente si servivano dell’abaco, dato che sfruttano appieno la potenza del sistema posizionale.

Dunque, fu solo nel corso del XIII secolo che cominciò lentamente e con difficoltà a diffondersi in Europa il calcolo aritmetico scritto che sostituì gradualmente l’uso dell’abaco. Il nuovo calcolo veniva chiamato algoritmo dal nome del matematico persiano Muḥammad ibn Mūsā al-Khwārizmī (ca. 780–850), autore di un trattato di aritmetica scritto verso l’830 e tradotto in latino con il titolo Algoritmi de numero Indorum (spesso tradotto: Sul calcolo numerico degli Indi).

Un notevole impulso alla diffusione delle nuove tecniche di calcolo fu dato anche dall’invenzione della stampa e, dunque, della maggior diffusione dei trattati di aritmetica che affrontavano questo tema. Tutti gli storici concordano sul fatto che il primo trattato a stampa di aritmetica apparve a Treviso nel 1478, L’arte de labbacho, meglio nota come Aritmetica di Treviso.

Fu una dura e strenua lotta quella che contrappose per buona parte del Medioevo e l’inizio del Rinascimento gli abacisti, strenui difensori del metodo degli antichi romani, che utilizzavano i sassolini, e gli algoritmisti, sostenitori del nuovo sistema posizionale di derivazione orientale, con l’uso dello zero e i calcoli fatti a mano con carta e calamaio. Questi ultimi trionfarono definitivamente soltanto nel corso del XVI secolo. Una lotta che per certi versi appare oggi analoga a quella tra il calcolo scritto e l’uso della calcolatrice elettronica.

Presentiamo un esempio di utilizzo di tale algoritmo. Supponiamo di voler moltiplicare 8'357 per 94. Disponiamo le cifre (usiamo quelle attuali) come indicato:

Eseguiamo ora i prodotti parziali, che naturalmente non avranno “riporti” dato che, al più, saranno formati da due cifre, e disponiamoli come segue:

Tracciamo ora tutte le diagonali dei rettangoli, congiungendo quelle contigue:

Addizioniamo ora i singoli termini seguendo le direzioni indicate dalle diagonali, e riportando, eventualmente, le cifre relative alle decine, alla successiva somma.

Otteniamo come risultato il numero richiesto: 785'558. Si noti la semplicità di questo algoritmo della moltiplicazione, la cui origine si perde nei tempi, e come sia simile al nostro attuale.

Un altro algoritmo che può essere utilizzato per svolgere la moltiplicazione è basato sull’uso di bastoncini cinesi. Riportiamo un esempio della moltiplicazione 23 x 12 = 276.

Ogni numero viene rappresentato da due gruppi di bacchette, rappresentanti le decine e le unità. I bastoncini relativi ai due numeri vengono sistemati in due diverse direzioni in modo che si incrocino tra loro. Nel nostro esempio le due bacchette che indicano le decine del 23 incontrano due volte la bacchetta che indica le decine del 12 e quattro volte le due bacchette che indicano le unità del 12.

Gli incroci tra le bacchette delle unità danno le unità del risultato (nell’esempio 6), gli incroci tra le bacchette delle unità e delle decine, sommati, indicano le decine del risultato (nell’esempio 4 + 3 = 7) mentre gli incroci delle bacchette delle decine indicano le centinaia (nell’esempio 2).

A partire dal 1500 le tecniche algoritmiche a carattere meccanico nascoste nei calcoli scritti fecero immaginare a menti geniali sempre più evolute macchine calcolatrici, precursore di quelle che intendiamo noi oggi, inventate soprattutto per sostituire l’impegnativo lavoro che doveva compiere il contabile nell’eseguire le operazioni aritmetiche.

È però solo attorno al 1970 che fecero la loro apparizione le macchine calcolatrici cosiddette elettroniche, assai più potenti, duttili ed economiche rispetto a quelle precedenti a manovella. Se a metà degli anni ‘50 del XX secolo nessuno o quasi possedeva una macchina calcolatrice, solo pochi anni dopo era impensabile non averne una: si è trattato di una rivoluzione sociale, relativa all’idea di calcolo, notevole, anche sul piano didattico. Sempre di più, infatti, furono i docenti che cominciarono a ritenere inutile dedicare ore, settimane, mesi, anni, sforzi all’apprendimento di algoritmi e all’esecuzione di calcoli da effettuarsi a mano. Fino agli anni ‘70 del XX secolo si usavano tavole scritte per il calcolo dei logaritmi, tavole trigonometriche, regoli da ingegnere con approssimazioni ecc.; tutti strumenti completamente scomparsi dall’uso pratico comune che, semmai, si possono ammirare con curiosità nei musei specifici. Dal punto di vista scolastico, la prima reazione all’uso della calcolatrice in classe fu di allontanamento: guai a quegli studenti che avessero fatto uso delle calcolatrici per effettuare calcoli durante processi algoritmici o per compiere fasi della risoluzione di problemi. In seguito, lentamente, questi strumenti entrarono a far parte della vita di classe.

Il vero sconvolgimento si ebbe però con l’ingresso in scena di due veri e propri geni della matematica, Alan Turing (1912-1954). e John von Neumann (1903-1957), che favorirono l’invenzione del moderno computer (1946), entrato ormai con forza nella nostra società.