Altri sistemi numerici

Sono diversi i sistemi numerici che si sono susseguiti nella storia e che sono stati scelti dalle diverse culture: uno dei primi di cui si è a conoscenza è basato sull’uno, il due e il molto. Uno rappresentava l’unità, due la coppia, e molto rappresentava parecchi o una moltitudine che serviva per parlare di tutte le altre quantità a partire dal tre. Non è un caso che la radice comune alle lingue semitiche “tr”, che significa originalmente “molto”, si ritrova ancora in lingue moderne a significare sia molto che tre, come per esempio in francese (très, trois).

Si sono poi diffusi diversi sistemi di numerazione ancorati a differenti basi: cinque (come le dita di una mano), dieci (che considera le dita di entrambe le mani), venti (che considera tutte le dita del nostro corpo), dodici (comoda dal punto di vista aritmetico, essendo il numero 12 divisibile per 1, 2, 3, 4, 6), sessanta (derivante da questioni legate al tempo e ai calendari) ecc. La base dodici veniva impiegata soprattutto nei sistemi commerciali di un tempo; di questo utilizzo ci restano oggi testimonianze nei termini dozzina e grossa (dozzina di dozzine), usate tuttora per uova e ostriche. La base sessanta, detta sessagesimale, viene ancora utilizzata per le ampiezze degli angoli e per misurare il tempo.

Nella storia si sono susseguiti sistemi additivi, nei quali il valore del numero era dato dall’addizione del valore di ogni simbolo, come quello degli Egizi, Greci, Etruschi, Romani, e sistemi posizionali come il nostro. Con ogni probabilità, il primo sistema posizionale della storia risale ai Sumeri; tale sistema è stato assunto in seguito dai Babilonesi e perfezionato infine dagli Indiani. Un sistema numerico posizionale a base venti mista (la venti e la cinque insieme) fu ideato dai Maya. Un vero e proprio sistema numerico posizionale a base dieci da cui deriva il nostro fu creato in India nel 500, arrivò presso gli Arabi nell’800 e giunse in Europa solo nel 1202.

È tramite il confronto tra il nostro sistema numerico decimale e differenti sistemi scelti da altre culture o utilizzati in diversi periodi storici, che è possibile comprendere con più profondità le caratteristiche e le potenzialità di quello utilizzato da noi oggi e capire che le scelte in tale ambito non sono univoche. Risulta sorprendente, per chi non ha mai visto alternative, comprendere che ci sono diverse strade per approcciare la rappresentazione e l’impostazione di un sistema numerico e non solo quella che abbiamo appreso noi fin da piccoli. Si apre così lo sguardo degli allievi su punti di vista diversi dai propri, cogliendo i limiti e le potenzialità di ciascun sistema.

È interessante analizzare inizialmente la tecnica utilizzata dagli uomini primitivi basata su tacche rappresentate su ossa o bastoni, così da intuire quanto risulta laborioso rappresentare 18 oggetti con ben 18 tacche, invece di utilizzare soli due simboli: 1 e 8, nel nostro sistema. Gli allievi inizieranno così ad intuire l’efficacia del nostro sistema posizionale.

È anche possibile introdurre il sistema additivo romano e l’affascinante sistema egizio per mostrarne i simboli, comprenderne le caratteristiche e il funzionamento, oltre a permettere interessanti accenni storici e geografici. I sistemi additivi utilizzati dai Romani e dagli Egizi rappresentano certamente un’evoluzione del sistema a tacche basato sulla corrispondenza biunivoca, ma possiedono certamente dei limiti, soprattutto a livello algoritmico, rispetto a quello che utilizziamo noi oggi.

È anche possibile proporre sistemi posizionali alternativi rispetto al nostro, come quello Babilonese o l’efficace sistema dei Maya, mettendo in evidenza scelte alternative di basi, di numero di cifre e di uso dello zero. Proporre altri sistemi numerici consente anche di far esercitare gli allievi su conteggi e calcoli in contesti stimolanti e diversi dalla routine. Va però considerato che è solo nel secondo ciclo che il confronto diventa ricco e profondo. 

Risulta inoltre molto interessante per la formazione globale dell’individuo collocare tali sistemi numerici nel periodo storico e nei luoghi del mondo dove effettivamente si sono sviluppati.

Riportiamo di seguito alcuni esempi di sistemi di numerazione adottati da altre culture nella storia, che possono risultare interessanti da essere proposti in classe.

Sumeri

Dopo la pratica degli intagli, tra i primi veri e propri documenti storici legati a sistemi numerici, vi sono numerosissime tavolette d’argilla risalenti alla civiltà sumerica, rintracciate in epoca relativamente recente in Mesopotamia, la terra fra i due fiumi Tigri ed Eufrate. I Sumeri, la cui origine si perde in epoche preistoriche, dominarono queste terre fino alle soglie del II millennio a. C. Risale a loro, con ogni probabilità, il primo sistema posizionale della storia dell’uomo. Le prime cifre sumere comparvero tra il 3300 e il 2850 a. C. e furono adottate in Mesopotamia dal 2500 a. C.

Il loro sistema numerico era misto, parte in base sessagesimale e parte in base decimale, e si fondava su un criterio additivo, per cui al valore di ogni simbolo andava aggiunto quello del simbolo immediatamente successivo: giunti a sommare l’ultimo simbolo, si otteneva così il valore dell’intero numero.

Essi avevano come unità di conto il piccolo cono, la piccola sfera, il grande cono, il grande cono perforato, la grande sfera e la grande sfera perforata. I valori relativi corrispondevano a 1, 10, 60, 600, 3‘600, 36‘000.

Per esempio, se si vuole scrivere 2'572, si deve innanzitutto notare che:

2'572 = 4 × 600 + 2 × 60 + 5 × 10 + 2 × 1.

Utilizzando i simboli della civiltà sumerica: 4 volte il grande cono perforato, 2 volte il grande cono, 5 piccole sfere e 2 piccoli coni; 2'572 si scrive si scrive nel seguente modo, con le unità disposte a sinistra:

Il principio è simile a quello dell’attuale sistema decimale, tuttavia la posizione dei simboli non rappresentava potenze a coefficienti successivi del 60, essendo il sistema anche additivo, e non era specificata una regola precisa e definitiva. Inoltre, i simboli del piccolo cono o del grande cono, così come quelli della piccola sfera o della grande sfera, avevano la stessa forma, variava solo la dimensione, dunque potevano essere confusi tra loro, soprattutto nel caso in cui non fossero entrambi presenti nel numero rappresentato. Chi leggeva la tavoletta doveva intuire l’ordine di grandezza basandosi sulle informazioni che aveva in merito al problema. Per questo a volte i segni numerali venivano accompagnati da logogrammi che servivano ad indicare gli oggetti conteggiati (per esempio, panieri di cibo destinati ai lavoratori), così da poter intuire a seconda della loro natura l’ordine di grandezza coinvolto.

Babilonesi

Nel frattempo, la fertile e ricca terra dei Sumeri venne invasa dai Babilonesi. Essi introdussero, accanto alla scrittura sumera, quella cuneiforme, cioè a forma di cuneo, assai più interessante. Per un certo periodo le due scritture convissero, ma in seguito la scrittura cuneiforme prese il sopravvento consolidandosi soprattutto nel periodo della ricca e florida dinastia degli Hammurabi (tra il 1800 e il 1600 a. C.). I Babilonesi usavano un sistema sessagesimale posizionale, non possedevano inizialmente un simbolo per lo zero e scrivevano i numerali come combinazioni di due soli simboli:

• il “chiodo verticale” o “cuneo” per le unità,

• il “punzone” con la punta diretta a sinistra o “angolo” per le decine.

Questi simboli (formati in modo additivo) venivano usati come “cifre” in un sistema sessagesimale posizionale. Ciò significa che, una volta arrivati a 60, questi 59 simboli venivano usati di nuovo per indicare le sessantine. Così:

1 sessantina era rappresentata da un cuneo,

2 sessantine erano rappresentate da due cunei,

3 sessantine erano rappresentate da tre cunei,

e via così.

Vi era quindi lo stesso simbolo per l’1 e per il 60, e questa volta della stessa dimensione, quindi a maggior ragione per comprendere l’ordine di grandezza di ciò che si voleva quantificare occorreva risalire al contesto e lavorare sulla posizione.

Ad esempio, 62 veniva rappresentato nel seguente modo, dove il primo cuneo indica una sessantina, ossia un’unità di ordine superiore e gli altri due cunei l’unità semplice:

Appositi simboli costituiti da cunei e angoli disposti in determinati modi indicavano ciascuno i seguenti numeri: 1, 10, 60, 600, 3'600, 36'000. Ad esempio, il 600 veniva rappresentato con due cunei perpendicolari nel seguente modo:

Solo al tempo di Alessandro Magno, nel IV secolo a. C., comparvero due cunei inclinati per indicare una posizione vuota per lo zero che veniva messa solo nelle posizioni intermedie, ma mai alla fine di un numero. Per le difficoltà implicite del sistema, la matematica di quelle civiltà rimase dominio quasi esclusivo della classe sacerdotale, depositaria della cultura e del potere.

Egizi

Assai florida fu la lunghissima e pacifica civiltà egizia che si sviluppò attorno al fiume Nilo, considerato un vero e proprio dono degli dèi. Per quanto riguarda l’aritmetica, gli antichi Egizi utilizzarono due diverse modalità di scrittura, la geroglifica e la ieratica, e svilupparono una grande sensibilità per le frazioni, purché il numeratore fosse rappresentato dall’unità.

La scrittura geroglifica fu la più antica, databile tra il 3300 e il 2850 a. C.; tale scrittura era basata su un sistema additivo, nel quale i simboli venivano ripetuti tante volte quanto necessario e la loro posizione (anche se rispettata) non era determinante per interpretare il valore del numero rappresentato. Tale scrittura non faceva uso di alcun simbolo per lo zero e privilegiava il 10; esistevano infatti segni speciali per indicare ciascuna delle prime sette potenze di 10, e per questa ragione con le cifre geroglifiche egiziane era possibile rappresentare numeri fino ad oltre un milione.

I simboli dei numerali egizi di tipo geroglifico erano i seguenti:

I simboli di ordine decimale più elevato erano scritti a destra di quelli di ordine minore. Il numero 743 veniva quindi rappresentato nella sequenza come se fosse scritto, nella nostra attuale scrittura, 347.

La scrittura numerale di quel lontano periodo storico è testimoniata dai papiri e dai documenti arrivati fino a noi e salvatisi dalle varie e ripetute distruzioni belliche. Il più citato è il cosiddetto “papiro di Ahmes” o “di Rhind”, datato 1650 a. C. e rintracciato solo nel 1858. Tra i più curiosi documenti ritrovati, ricordiamo l’estremità di una mazza risalente all’inizio del III millennio a. C. che contiene la registrazione dei bottini di guerra del faraone Narmer: ben 400'000 bovini, 1'422'000 ovini e 120'000 prigionieri.

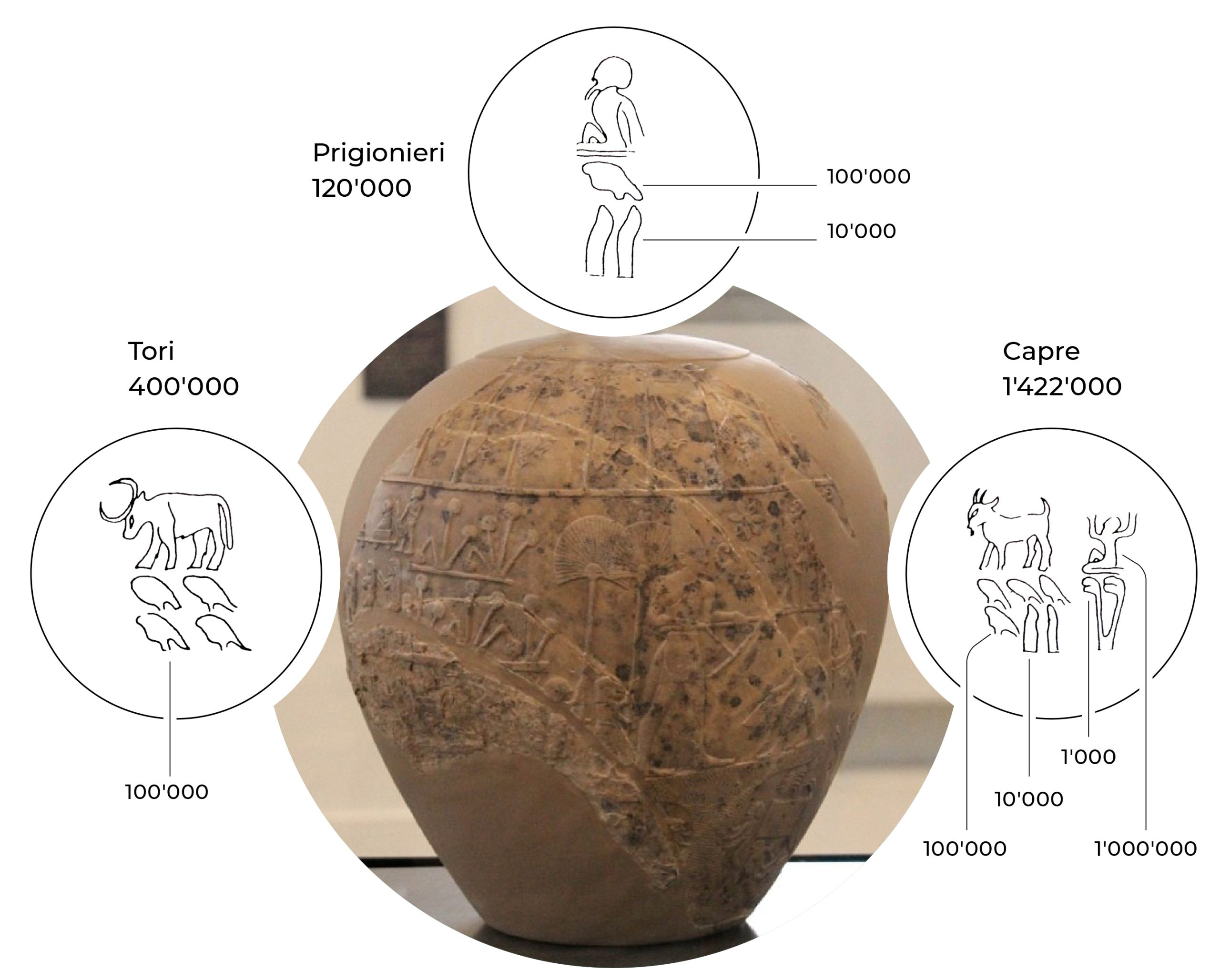
Questa era la forma geroglifica di scrittura dei numerali più diffusa, ma non era univoca; in diverse epoche, in diversi luoghi e su diversi materiali, si sono trovate anche forme di scrittura assai diverse.

Ben nota è inoltre la cosiddetta stele di Nefertiabet (figlia del faraone Cheope, morta attorno al 2590 a. C.) che rappresenta ed enumera i beni che la sua anima portò con sé nel passaggio al regno dei morti.

Alla scrittura geroglifica, ingombrante, difficile, lenta e faticosa, si contrappose l’assai più snella scrittura “ieratica”. Tale scrittura ieratica veniva usata più spesso di quella geroglifica sia dai sacerdoti sia dagli scribi, soprattutto per effettuare conti, stendere censimenti, inventari, rapporti, testamenti, atti amministrativi ecc.

Ecco i simboli ieratici che appaiono nel papiro di Rhind:

Romani

I multipli di I, X, C e M si esprimevano ripetendo i segni corrispondenti, ma solo fino a quattro volte: IIII cioè 4 volte 1, MM cioè 2 volte 1'000 ecc. I numeri scritti a destra di un numero superiore andavano sommati allo stesso; si trattava dunque di un sistema additivo:

XII = 10 + 2 × 1 = 12,

MCCLXXXVI = 1'000 + 2 × 100 + 50 + 3 × 10 + 5 + 1 = 1'286.

Più tardiva è l’idea sottrattiva: i segni I, X, C, se posti a sinistra di un numero superiore, indicavano che dovevano essere sottratti a quel numero:

IV = 5 – 1 = 4,

CD = 500 – 100 = 400.

Il segno D si trova a volte sostituito da IƆ; aggiungendo ancora il segno Ɔ a destra, il numero si intendeva moltiplicato per 10: IƆ = 500, IƆƆ = 5'000, IƆƆƆ = 50'000. Allo stesso modo, il segno M poteva essere scritto CIƆ; per moltiplicare per 10, 100 ecc. si aggiungeva una coppia di segni da ambo le parti:

CIƆ = 1'000,

CCIƆƆ = 10'000,

CCCIƆƆƆ = 100'000.

La moltiplicazione per mille si indicava sopralineando il numero:

XL = 40 e XL = 40'000;

L = 50 e L = 50'000.

Infine, se oltre alla sopralineatura, il numero era sbarrato da ambo le parti, si intendeva moltiplicato per 100'000:

|V| = 500'000,

|C| = 10'000'000.

I segni ausiliari | |, ‾‾, Ɔ risultavano molto efficienti per rappresentare numeri con le ultime cifre uguali a zero; ma si pensi di dovere scrivere, ad esempio, 1'849'679: un’impresa!

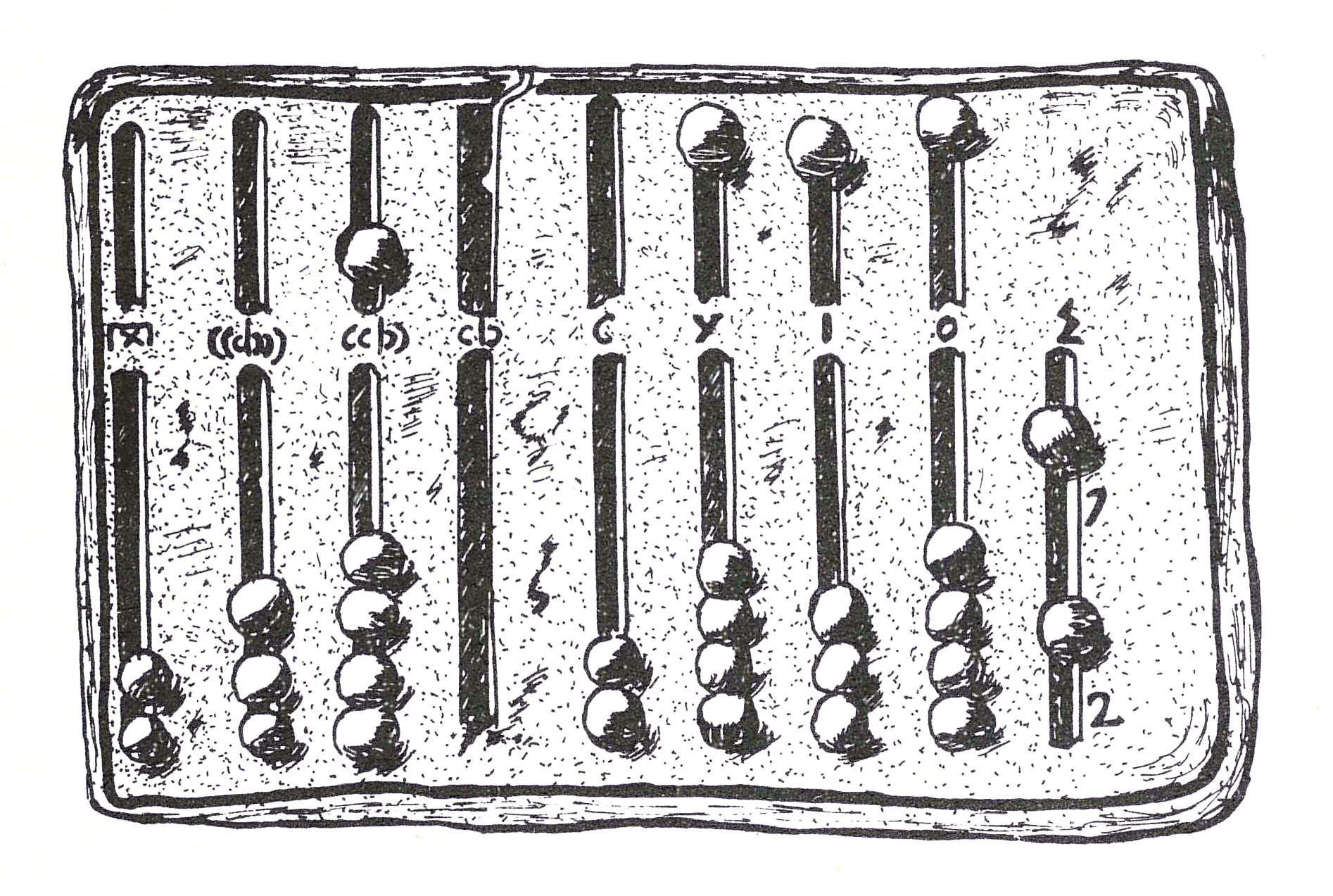
Alla scrittura complessa delle entità numeriche, si sovrapponeva un’altra notevole difficoltà, di tipo algoritmico. Per rispondere a queste problematiche, i Romani, come i Greci e senz’altro gli Etruschi, dovettero dunque ricorrere a macchine da calcolo, gli abachi (si veda il contenuto Strategie di calcolo).

Maya

Tra i diversi sistemi di numerazione che si sono sviluppati nella storia, certamente uno dei più interessanti è quello della civiltà maya, che fiorì fra il 300 a. C. e il 900, in quello che fu detto il periodo classico, in una zona situata oggi nella parte più meridionale del Nordamerica e nel Centroamerica. A questo periodo seguì quello postclassico che durò fino alla conquista spagnola del XVI secolo.

Il sistema maya era posizionale, un sistema cioè in cui il valore delle cifre è determinato dalla loro posizione nella scrittura del numero, e si basava su una base mista: la 5 e la 20 insieme, ma con prevalenza della 20. Il 5 rappresenta le dita di una mano o dei piedi, il 20 l’intero numero delle dita del corpo umano (mani più piedi); in effetti, nella storia molte tribù che non usavano le scarpe hanno sfruttato anche le dita dei piedi per poter contare e per questo ragionavano in base 20.

Come strumenti per contare, i Maya utilizzavano fagioli (in spagnolo: frijolitos) o chicchi di mais o legnetti (in spagnolo: palitos). Usavano quindi solo 3 diverse cifre: il fagiolo per indicare l’1, il legnetto per indicare il 5 e un simbolo per lo zero.

Recenti studi concordano nel riconoscere che furono proprio i Maya i primi a utilizzare in modo esplicito lo zero come numero; esso veniva rappresentato in diversi modi, e lo si chiamava a volte “ombelico”, ma più spesso “conchiglia”.

Questa notazione numerica posizionale andava dal basso verso l’alto, invece che da destra a sinistra come la nostra, incolonnando i simboli verticalmente. Il primo livello o ordine indicava le unità, il secondo livello, che si trovava sopra il primo, indicava le ventine, il terzo livello rappresentava l’ordine di grandezza 20 × 20 e così via. In realtà spesso si utilizzava come terzo livello, al posto di 20 × 20, 20 × 18 (360), sotto l’influenza dal conteggio del tempo che, nella vita maya, era davvero importante. La posizione che per noi è rappresentata da decine per loro era rappresentata da ventine.

Il 20 nel sistema maya veniva quindi rappresentato nel seguente modo, zero unità e una ventina (il numero viene letto dal basso verso l’alto):